Multiple View Geometry in Computer Vision Chapter 2 Solutions

Here’s a quick index to all the problems in this chapter.

i ii iii iv v vi viii ix

The main index can be found here.

I. (a) Show that an affine transformation can map a circle to an ellipse, but cannot map an ellipse to a hyperbola or parabola.
(b) Prove that under an affine transformation the ratio of lengths on parallel line segments is an invariant, but that the ratio of two lengths that are not parallel is not.

(a) All affine transformations that have non-isotropic scaling will result in a circle being stretched and squashed into an ellipse. For example, the following affine transformation will cause such an effect. $$\begin{pmatrix} 10 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Next, let’s prove the more general result. From Eq 2.3 (Pg. 30), the quadratic equation of a general conic can be represented in matrix form as follows. $$C = \begin{pmatrix} a & b/2 & d/2 \\ b/2 & c & e/2 \\ d/2 & e/2 & f \end{pmatrix}$$

The euclidean classification of a conic is based on the determinant of the upper-left 2x2 matrix of its quadratic form. This value, $ac - \frac{b^2}{4}$, is also called the discriminant of the conic section. If the discriminant is 0 then the conic is classified as a parabola, if it is positive an ellipse and if negative a hyperbola.

To find the classification of a conic after an affine transformation, let’s find the discriminant of the transformed conic. The equation of transformation of a conic under a point transformation is given by $C’ = H^{-T}CH^{-1}$ (Result 2.13). As the inverse of an affine transformation is also an affine transformation ¹ we can write the transformed conic as $$C’ = \begin{pmatrix} A^T & 0 \\ \textbf{p}^T & 1 \end{pmatrix} \begin{pmatrix} a & b/2 & d/2 \\ b/2 & c & e/2 \\ d/2 & e/2 & f \end{pmatrix} \begin{pmatrix} A & \textbf{p} \\ 0 & 1 \end{pmatrix}.$$

The discriminant of this transformed conic will be the determinant of the following sub-matrix. $$A^T\begin{pmatrix}a & b/2 \\ b/2 & c\end{pmatrix}A$$

As the determinant of the transpose of a matrix is the same as that of the matrix itself, the above mentioned determinant will be $(det(A))^2(ac - \frac{b^2}{4})$. As the square term will always be positive, this discriminant will be 0 when $\frac{b^2}{4} = ac$, positive when $\frac{b^2}{4} < ac$ and negative when $\frac{b^2}{4} > ac$. Hence the classification of the affinely transformed conic is the same as the classification of the original conic and an ellipse can only be transformed to an ellipse and never to a parabola or a hyperbola under an affine transformation.

(b) The proof for this is directly taken from the book “Introduction to Projective Geometry” by C.R. Wylie, Jr, Section 5.10, Theorem 3 Proof. I really like this book and highly recommend it to anyone who wants to learn projective geometry for computer vision.

Let $U: (u_1, u_2, 1)$ and $V: (v_1, v_2, 1)$ be two points which are not on the ideal line, and let $U’: (u’_1, u’_2, 1)$ and $V: (v’_1, v’_2, 1)$ be their images under an arbitrary affine transformation

$$x’_1 = a_{11}x_1 + a_{12}x_2 + a_{13}x_3$$ $$x’_2 = a_{21}x_1 + a_{22}x_2 + a_{23}x_3$$ $$x’_3 = x_3$$

Then by an easy calculation we find $$v’_1 - u’_1 = a_{11}(v_1 - u_1) + a_{12}(v_2 - u_2)$$ $$v’_2 - u’_2 = a_{21}(v_1 - u_1) + a_{22}(v_2 - u_2)$$

The square of the ratio of the distance $(U’V’)$ to the distance $(UV)$ is therefore

$$\frac{(a_{11}^2 + a_{21}^2)(v_1 - u_1)^2 + 2(a_{11}a_{12} + a_{21}a_{22})(v_1 - u_1)(v_2 - u_2) + (a_{12}^2 + a_{22}^2)(v_2 - u_2)^2}{(v_1 - u_1)^2 + (v_2 - u_2)^2}$$

If $(v_1 - u_1) = 0$, this expression reduces to $a_{12}^2 + a_{22}^2$, which depends only on the coefficients in the equation of the given transformation. On the other hand, if $(v_1 - u_1) \ne 0$, we can divide the numerator and the denominator of the last fraction by $(v_1 - u_1)^2$. Then, noting that $\frac{v_2 - u_2}{v_1 - u_1}$ is just the slope, $m$, of the line which contains the segment $\overline{UV}$, we have $$\frac{(U’V’)^2}{(UV)^2} = \frac{(a_{11}^2 + a_{21}^2) + 2(a_{11}a_{12} + a_{21}a_{22})m + (a_{12}^2 + a_{22}^2)m^2}{1 + m^2}.$$

Since this depends only on the coefficients in the equations of the transformation and the slope of the given segment, we can conclude that an affine transformation multiplies the lengths of all segments in a given direction by a factor which depends only on the transformation and the given direction.

This directly implies that under an affine transformation the ratio of lengths on parallel line segments is an invariant (as both have the same value for the slope $m$), but that the ratio of two lengths that are not parallel is not (as they have different values for the slope $m$).

II. Projective transformations. Show that there is a three-parameter family of projective transformations which fix (as a set) a unit circle at the origin, i.e. a unit circle at the origin is mapped to a unit circle at the origin. What is the geometric interpretation of this family?

The equation of transformation of a conic under a point transformation is given by $C’ = H^{-T}CH^{-1}$ (Result 2.13).

If $C$ is the matrix of the quadratic form of a unit circle then

$$C = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{pmatrix}$$

A transformation that preserves a unit circle will satisfy the condition $$H^{-T}CH^{-1} = kC$$ where $k$ is an arbitrary scale factor.

As $H$ represents an equivalence class, it is no specialization to set $k = 1$.

Inverting both sides and noting that $C^{-1} = C$ we get

$$HCH^T = C$$

Expanding this, we get

$$\begin{pmatrix} h_{11}^2 + h_{12}^2 - h_{13}^2 & h_{12}h_{22} + h_{11}h_{21} - h_{13}h_{23} & h_{12}h_{32} + h_{11}h_{31} - h_{13}h_{33} \\ h_{12}h_{22} + h_{11}h_{21} - h_{13}h_{23} & h_{21}^2 + h_{22}^2 - h_{23}^2 & h_{22}h_{32} + h_{21}h_{31} - h_{23}h_{33} \\ h_{12}h_{32} + h_{11}h_{31} - h_{13}h_{33} & h_{22}h_{32} + h_{21}h_{31} - h_{23}h_{33} & h_{31}^2 + h_{32}^2 - h_{33}^2 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{pmatrix}$$

This linear system results in a total of 6 unique constraints on the 10 unknowns. $$h_{11}^2 + h_{12}^2 - h_{13}^2 = 1$$ $$h_{12}h_{22} + h_{11}h_{21} = h_{13}h_{23}$$ $$h_{12}h_{32} + h_{11}h_{31} = h_{13}h_{33}$$ $$h_{21}^2 + h_{22}^2 - h_{23}^2 = 1$$ $$h_{22}h_{32} + h_{21}h_{31} = h_{23}h_{33}$$ $$h_{31}^2 + h_{32}^2 - h_{33}^2 = -1$$

This system then has $9 - 6 = 3$ degrees of freedom and hence $H$ can represent a three-parameter family of projective transformations.

To understand the geometric interpretation of this family of transformations let’s look at the problem in a different manner. Consider the linear system system in 2D that we wish to solve to obtain the constraints on $H$.

$$HCH^T = C$$

An equivalent way² to solve for this H would be to solve the following system of equation in 3D.

$$\begin{pmatrix} H & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} C & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} H^T & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} C & 0 \\ 0 & 1 \end{pmatrix}$$

or,

$$\begin{pmatrix} HCH^{T} & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} C & 0 \\ 0 & 1 \end{pmatrix}$$

This means that the set of projective transformations in 2D that preserve a unit circle $C$ at the origin is the same as the set of affine transformations that preserves the quadric represented by $\begin{pmatrix} C & 0 \\ 0 & 1 \end{pmatrix}$ in 3D.

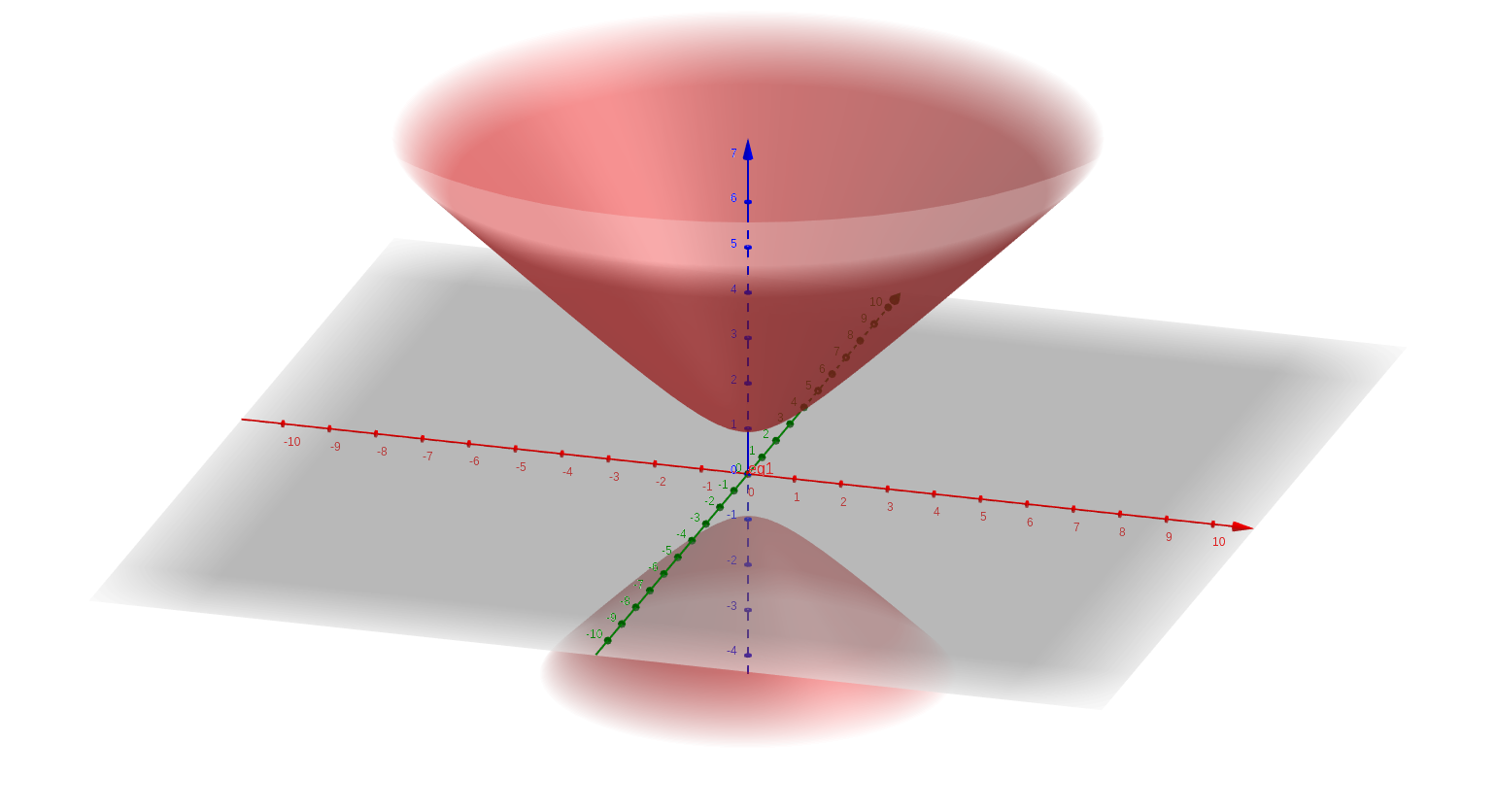
The quadric $\begin{pmatrix} C & 0 \\ 0 & 1 \end{pmatrix}$ or $\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$ is a two-sheeted hyperboloid $x^2 + y^2 - z^2 + 1 = 0$.

The only types of affine transformations that can preserve a shape and its position as a whole are rotations and reflections (similarity transformations). We can immediately see that this hyperboloid has rotational symmetry about the z-axis (in blue). Hence any rotation about the origin along this axis will preserve the hyperboloid. This transformation in homogeneous form is as follows.

$$\begin{pmatrix} cos(\theta) & -sin(\theta) & 0 & 0 \\ sin(\theta) & cos(\theta) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

Similarly, the hyperboloid has mirror symmetry about planes passing through the origin and perpendicular to the $xy$ plane. This transformation in homogeneous form is as follows.

$$\begin{pmatrix} cos(\alpha) & sin(\alpha) & 0 & 0 \\ sin(\alpha) & -cos(\alpha) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

where $\alpha$ is the angle made by the plane with the $xz$ plane.

Another type of “rotation” that we don’t usually encounter, possibly because we perceive the world around us as euclidean and measure distance using a euclidean metric, is a class of transformations known as hyperbolic rotations. This hyperboloid will be preserved by such hyperboloid rotations in 3D about the x and y axes³. These transformations in homogeneous form are as follows. $$\begin{pmatrix} cosh(\beta) & 0 & sinh(\beta) & 0 \\ 0 & 1 & 0 & 0 \\ sinh(\beta) & 0 & cosh(\beta) & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$

$$\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & cosh(\gamma) & sinh(\gamma) & 0 \\ 0 & sinh(\gamma) & cosh(\gamma) & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$$ where $cosh$ and $sinh$ are the hyperbolic cosine and sine functions, and $\beta$ and $\gamma$ are the hyperbolic angles through which the points are rotated. These transformations are also known as Lorentz transformations.

Correspondingly, the following types of transformations will preserve the unit circle centered at the origin. $$\begin{pmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

$$\begin{pmatrix} cos(\alpha) & sin(\alpha) & 0 \\ sin(\alpha) & -cos(\alpha) & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

$$\begin{pmatrix} cosh(\beta) & 0 & sinh(\beta) \\ 0 & 1 & 0 \\ sinh(\beta) & 0 & cosh(\beta) \end{pmatrix}$$

$$\begin{pmatrix} 1 & 0 & 0 \\ 0 & cosh(\gamma) & sinh(\gamma) \\ 0 & sinh(\gamma) & cosh(\gamma) \end{pmatrix}$$

Although we see 4 different types of transformations which preserve the hyperboloid, only 3 of them are independent. This is because any rotation can be expressed as a composition of reflections.

It is important to note that the last two transformations are hyperbolic rotations in 3D, not in 2D and hence do not have a specific geometric interpretation in 2D.

In conclusion, we can express any transformation which preserves the unit circle by a composition of three types of transformations, parameterized by three independent parameters $\alpha, \beta,$ and $\gamma$. This is consistent with the result obtained by looking at the system of linear equations.

III. Isotropies. Show that two lines have an invariant under a similarity transformation; and that two lines and two points have an invariant under a projective transformation. In both cases the equality of the counting argument (result 2.16) is violated. Show that for these two cases the respective transformation cannot be fully determined, although it is partially determined.

Under a similarity transform, angles are left unchanged. So, in the first case, the angle made by the two lines is an invariant under the similarity transformation. To uniquely determine an orientation preserving similarity transform, we only need 2 pairs of points or 2 pairs of lines. But to uniquely determine a similarity transform we need 3 pairs of points or 3 pairs of lines, one extra to determine whether the transformation is orientation preserving or reversing. Hence there will be two similarities that perform the given transformation.

For the second case, let’s call the two points $P$ and $Q$. Let the intersection of the two given lines with the line $PQ$ be $R$ and $S$. Then $P$, $Q$, $R$ and $S$ are collinear (all lie on $PQ$) and their cross ratio will be preserved by a projective transformation. To uniquely determine a projective transformation, which has 8 degrees of freedom, we need 4 pairs of points (or 4 pairs of lines). Here, we are given only 3 and hence a projective transformation can not be fully determined in this case. This means there are an infinite number of projective transformations that achieve the given mapping.

For more information about invariant theory relevant to computer vision please see “Projective Invariants for Vision” ⁴.

IV. Invariants. Using the transformation rules for points, lines and conics show:
(a) Two lines $l_1$, $l_2$, and two points $x_1$, $x_2$, not lying on the lines have the invariant $$I = \frac{(l_1^Tx_1)(l_2^Tx_2)}{(l_1^Tx_2)(l_2^Tx_1)}$$
(b) A conic $C$ and two points $x_1$ and $x_2$, in general position have the invariant $$I = \frac{(x_1^TCx_2)^2}{(x_1^TCx_1)(x_2^TCx_2)}$$
(c) Show that the projectively invariant expression for measuring angles (2.22) is equivalent to Laguerre’s projectively invariant expression involving a cross ratio with the circular points.

(a) Under a projective transformation, the quantity $l^Tx$ transforms to $(H^{-T}l)^THx = l^TH^{-1}Hx = l^Tx$. Hence the given ratio will be invariant under a projective transform.

(b) Under a projective transformation, the quantity $x_1^TCx_2$ transforms to $(Hx_1)^T(H^{-T}CH^{-1})Hx_2 = x_1^TH^TH^{-T}CH^{-1}Hx_2 = x_1^TCx_2$. Hence the given ratio will be invariant under a projective transform.

(c) Laguerre’s cross ratio involves 4 concurrent lines: the two given lines and the lines joining the intersections of the two given lines with the circular points. We can translate the origin to the point of intersection of the two lines without changing the coordinates of the circular points as translation is a similarity transform and similarity transforms leave the circular points invariant. This transform also leaves the cross ratio invariant as it is a perspective transform. This way we can get rid of the intercepts and simplify the arithmetic involved.

Let the two lines be $A: [l_1, l_2, 0]$ and $B: [m_1, m_2, 0]$. Then their point of intersection will be $(0, 0, l_1m_2 - l_2m_1)$. The lines joining this point with the circular points will be $C: [-i, 1, 0]$ and $D: [i, 1, 0]$.

Let the base lines be $C$ and $D$, so that their parameters are $(1, 0)$ and $(0, 1)$ respectively. Then the parameters of $A$ and $B$ with respect to the base points will be $A: (\frac{-l_2 - il_1}{2}, \frac{-l_2 + il_1}{2})$, $B: (\frac{-m_2 - im_1}{2}, \frac{-m_2 + im_1}{2})$. The cross ratio of these 4 points will then be $$\frac{\begin{vmatrix} 1 & 0 \\ \frac{-m_2 - im_1}{2} & \frac{-m_2 + im_1}{2} \end{vmatrix} \begin{vmatrix} 0 & 1 \\ \frac{-l_2 - il_1}{2} & \frac{-l_2 + il_1}{2} \end{vmatrix}} {\begin{vmatrix} 1 & 0 \\ \frac{-l_2 - il_1}{2} & \frac{-l_2 + il_1}{2} \end{vmatrix} \begin{vmatrix} 0 & 1 \\ \frac{-m_2 - im_1}{2} & \frac{-m_2 + im_1}{2} \end{vmatrix}}$$

$$= \frac{(-m_2 + im_1)(l_2 + il_1)}{(-l_2 + il_1)(m_2 + im_1)}$$

$$= \frac{m_1l_1 + m_2l_2 + i(m_1l_2 - m_2l_1)}{m_1l_1 + m_2l_2 + i(m_2l_1 - m_1l_2)}$$

$$= \frac{1 + i\frac{m_1l_2 - m_2l_1}{m_1l_1 + m_2l_2}}{1 + i\frac{m_2l_1 - m_1l_2}{m_1l_1 + m_2l_2}}$$

To get the logarithm in the picture, we need to convert these coordinates from rectangular to polar. In polar coordinates, this equation is equivalent to $$\frac{r(cos(\theta) + isin(\theta))}{r(cos(-\theta) + isin(-\theta))}$$ $$= \frac{cos(\theta) + isin(\theta)}{cos(-\theta) + isin(-\theta)}$$ $$= \frac{e^{i\theta}}{e^{-i\theta}}$$ $$= e^{2i\theta}$$

where $\theta = tan^{-1}(\frac{m_1l_2 - m_2l_1}{m_1l_1 + m_2l_2}) = cos^{-1}(\frac{m_1l_1 + m_2l_2}{\sqrt{(m_1^2 + m_2^2)(l_1^2 + l_2^2)}})$. This is the same as the result in 2.21 and 2.22.

In other words, if we know the cross ratio of two lines and the lines joining their point of intersection to the two circular points, we can calculate the euclidean angle $\theta$ between the lines using the following relation

$$\theta = |\frac{1}{2i}log(crossratio(A, B, C, D))|$$

As the cross ratio is projectively invariant, this quantity is too.

This result was first discovered in 1853 by the French mathematician Edmond Laguerre (1834-1886), who was the first to recognize the relation between cross ratios and the measurement of angles. - Introduction to Projective Geometry, C.R. Wylie, Jr.

V. The cross ratio. Prove the invariance of the cross ratio of four collinear points under projective transformations of the line (2.18).

Consider the term

$$|\bar{x}’_i\bar{x}’_j|$$

Rewriting this in terms of $\bar{x}_i$ and $\bar{x}_j$, we get

$$|\bar{x}’_i\bar{x}’_j| = \begin{vmatrix}\lambda_iH_{2\times2}\bar{x}_i & \lambda_jH_{2\times2}\bar{x}_j \end{vmatrix}$$

$$= |H_{2\times2} \begin{pmatrix}\lambda_i\bar{x}_i & \lambda_j\bar{x}_j\end{pmatrix}|$$

As determinant of a product of matrices is the product of their respective determinants, we get

$$|H_{2\times2}| \begin{vmatrix}\lambda_i\bar{x}_i & \lambda_j\bar{x}_j\end{vmatrix}$$

Next, if all elements of a column of a determinant are multiplied by a scalar then the value of the determinant is $k$ times the given determinant. So the determinant becomes

$$= \lambda_i\lambda_j|H_{2\times2}| \begin{vmatrix}\bar{x}_i & \bar{x}_j\end{vmatrix}$$

Now consider the cross ratio

$$\frac{|\bar{x}’_1\bar{x}’_2||\bar{x}’_3\bar{x}’_4|}{|\bar{x}’_1\bar{x}’_3||\bar{x}’_2\bar{x}’_4|}$$

Rewriting this using the result above, we get

$$\frac{\lambda_1\lambda_2|H_{2\times2}||\bar{x}_1\bar{x}_2|\lambda_3\lambda_4|H_{2\times2}||\bar{x}_3\bar{x}_4|}{\lambda_1\lambda_3|H_{2\times2}||\bar{x}_1\bar{x}_3|\lambda_2\lambda_4|H_{2\times2}||\bar{x}_2\bar{x}_4|}$$

$$= \frac{\lambda_1\lambda_2\lambda_3\lambda_4|H_{2\times2}|^2|\bar{x}_1\bar{x}_2||\bar{x}_3\bar{x}_4|}{\lambda_1\lambda_2\lambda_3\lambda_4|H_{2\times2}|^2|\bar{x}_1\bar{x}_3||\bar{x}_2\bar{x}_4|}$$

$$=\frac{|\bar{x}_1\bar{x}_2||\bar{x}_3\bar{x}_4|}{|\bar{x}_1\bar{x}_3||\bar{x}_2\bar{x}_4|}$$

Hence the cross ratio is invariant under a projective transformation.

The alternate proof⁵ that the exercise refers to is done using pure trigonometry (the law of sines).

VI. Polarity. Give a geometric construction for the polar when the point is inside the ellipse.

To find the polar of a point inside the conic we will use the following two theorems.

1. The polar line of a point $x$ with respect to a conic intersects the conic in two points. The two lines tangent to the conic at these points intersect at $x$.
2. If $x$ is on the polar of $y$ then $y$ is on the polar of $x$.

In the given figure, we want to find the polar of point $F$ which lies inside the ellipse. This means the lines $HG$ and $IJ$ must be polars of points that lie on the polar of $F$. To find the points of which $HG$ and $IJ$ are the polars, we use theorem 1. The intersection of the tangents to the conic at $H$ and $G$ will given the point $L$ of which $HG$ is the polar. Similarly, the intersection of the tangents to the conic at $I$ and $J$ gives the point $K$ of which $IJ$ is the polar. The line that joins $L$ and $K$ is then the polar of $F$.

Summarizing this process, we get the following construction.

1. Draw two lines $l$ and $m$ through the point $F$ inside the ellipse.
2. Find their points of intersection with the conic. Let them be $H$ and $G$ for $l$ and $I$ and $J$ for $m$.
3. Find the points of intersection $L$, of tangents through $H$ and $G$, and $K$ of tangents through $I$ and $J$.
4. The line joining $L$ and $K$ is the polar of point $F$.

Now, you might be wondering how this line $LK$ follows theorem 1 as it doesn’t seem to be intersecting the ellipse at all. It does intersect the ellipse though, in complex points.

VIII. Dual conics. Show that the matrix $[l]_xC[l]_x$ represents a rank 2 dual conic which consists of the two points at which the line $l$ intersects the (point) conic $C$.

First, let’s prove that the matrix $[l]_xC[l]_x$ is the matrix of the quadratic form of a conic. We know that any symmetric matrix can be decomposed into the form $Q\Lambda Q^T$, where $Q$ is an orthogonal matrix of the eigenvectors of the symmetric matrix and $\Lambda$ is a diagonal matrix of the corresponding eigenvalues. This is called diagonalizing a symmetric matrix⁶. Substituting this for $C$, we get

$$[l]_xQ\Lambda Q^T[l]_x$$

$$= [l]_xQ\sqrt{\Lambda}\sqrt{\Lambda}Q^T[l]_x$$

$$= [l]_xQ\sqrt{\Lambda}\sqrt{\Lambda}^TQ^T[l]_x$$

As $[l]_x$ is skew-symmetric, $[l]_x = -[l]_x^T$ and this equation becomes

$$= -[l]_xQ\sqrt{\Lambda}\sqrt{\Lambda}^TQ^T[l]_x^T$$

$$= -([l]_xQ\sqrt{\Lambda})([l]_xQ\sqrt{\Lambda})^T$$

$$= -AA^T$$

where $A = [l]_xQ\sqrt{\Lambda}$.

As $AA^T$ is clearly a symmetric matrix, so is $-AA^T$. Hence $[l]_xC[l]_x$ is symmetric and represents the quadratic form of a conic.

Next, we’ll prove the conic $[l]_xC[l]_x$ is singular by using the fact that the determinant of a singular conic is 0.

The upper bound on the rank of a product of matrices is determined by the matrix with the lowest rank. In this case, we know that $[l]_x$ has rank 2. Hence the rank of the product $[l]_xC[l]_x$ can not be greater than 2. This further means that $[l]_xC[l]_x$ is not a full-rank matrix and that its determinant must be 0. Hence $[l]_xC[l]_x$ represents the quadratic form of a degenerate conic.

The next part of the proof is adapted from the book “Perspectives on Projective Geometry”⁷, another great book on projective geometry with a focus on practical algorithms.

All lines $m$ tangent to the conic $[l]_xC[l]_x$ must satisfy the equation

$$m^T[l]_xC[l]_xm = 0$$ $$\implies -m^T[l]_x^TC[l]_xm = 0$$ $$\implies m^T[l]_x^TC[l]_xm = 0$$ $$\implies ([l]_xm)^TC([l]_xm) = 0$$

But $[l]_xm$ denotes the cross product $l \times m$ (Appendix 4.2). So, all lines $m$ tangent to the singular conic must satisfy the following equation.

$$ (l \times m)^TC(l \times m) = 0$$

This means that the intersection of $l$ and any line $m$ that is tangent to the singular conic $[l]_xC[l]_x$ must lie on the conic $C$. If the line $l$ is itself tangent to the conic then there is only one such point else there are two such points. Hence the degenerate conic $[l]_xC[l]_x$ is composed of the points of intersection (which might not be distinct) of $l$ with the point conic $C$.

Note: The question assumes that $l$ intersects $C$ in two points, hence rank of the degenerate dual conic is 2. If $l$ was tangent to $C$ then the rank of $[l]_xC[l]_x$ would be 1.

IX. Special projective transformations. Suppose points on a scene plane are related by reflection in a line: for example, a plane object with bilateral symmetry. Show that in a perspective image of the plane the points are related by a projectivity $H$ satisfying $H^2 = I$. Furthermore, show that under $H$ there is a line of fixed points corresponding to the imaged reflection line, and that $H$ has an eigenvector, not lying on this line, which is the vanishing point of the reflection direction ($H$ is a planar harmonic homology).
Now suppose that the points are related by a finite rotational symmetry: for example, points on a hexagonal bolt head. Show in this case that $H^n = I$, where $n$ is the order of rotational symmetry (6 for a hexagonal symmetry), that the eigenvalues of $H$ determine the rotation angle, and that the eigenvector corresponding to the real eigenvalue is the image of the center of the rotational symmetry.

Reflective Symmetry

Let $x$ be any point on the scene plane. Then there will exist another point $Rx$, where $R$ is the matrix of reflection, that is the mirror image of $x$ on the scene plane. Applying the homography $A$ to both these points, we will get their images to be $Ax$ and $ARx$. The question asks us about a homography $H$ such that $HAx = ARx$ upto scale. This means $HA = AR$ and thus $H = ARA^{-1}$ up to scale.

Now $H^2$ will be $(ARA^{-1})(ARA^{-1})$.

$$\implies H^2 = AR(A^{-1}A)RA^{-1}$$ $$\implies H^2 = ARIRA^{-1}$$ $$\implies H^2 = AR^2A^{-1}$$ As applying a reflection operation twice results in the original point, $R^2 = I$. Thus, we get $$\implies H^2 = AIA^{-1}$$ $$\implies H^2 = AA^{-1}$$ $$\implies H^2 = I$$

Hence the points on the image of the scene will be related by a homography $H$ such that $H^2 = I$ up to scale, i.e. $H$ is an involution.

The image points $y’$ left unchanged by $H$ must satisfy the condition $ARA^{-1}y’ = y’$ up to scale. Representing the image by the original coordinates $y’ = Ay$, the condition becomes $ARA^{-1}Ay = Ay$ or $ARy = Ay$. This condition will only hold for those points $y$ on the scene plane that satisfy the condition $Ry = y$ up to scale.

One set of points that satisfy this condition are the points on the reflection line on the scene plane. Dually, the lines that are parallel to the reflection direction are left unchanged (not point-by-point) by $R$. Hence the point of intersection of all such parallel lines, the ideal point of the reflection direction, must be fixed under $R$. It follows, then, that the imaged reflection line is point-by-point invariant and vanishing point (imaged ideal point) of the reflection direction is a fixed point (eigenvector) of $H$.

So, $H$ has two repeated eigenvalues (corresponding to the fixed reflection line) and one distinct eigenvalue (corresponding to the vanishing point of the reflection direction), making it a homology; and as $H^2 = I$, it becomes a harmonic homology.

Rotational Symmetry

The logic behind this answer is pretty similar to the one above.

If $x$ is a point on the scene plane then there will be n other points $Rx$, $\ldots$, $R^nx$ that are identical to $x$, where $R$ is the matrix of rotation around the center of the rotational symmetry. Applying the homography $A$ to these points, we get $Ax$, $ARx$, $\ldots$, $AR^nx$. The question asks us about a homography $H$ such that $HAx = ARx$. This means $HA = AR$ and thus $H = ARA^{-1}$ up to scale.

Now $H^n$ will be $(ARA^{-1})\ldots(ARA^{-1})$ $n$ times.

$$\implies H^n = AR^nA^{-1}$$ As applying the rotation $n$ times results in the original point, $R^n = I$. Thus, we get $$\implies H^n = AA^{-1}$$ $$\implies H^n = I$$

Hence the points on the image of the scene will be related by a homography $H$ such that $H^n = I$ up to scale, i.e. $H$ is a collineation of period $n$.

As $H = ARA^{-1}$ it is similar to $R$. This means it will have the same eigenvalues as $R$. Taking the center of rotational symmetry as the origin of the coordinate system the rotation matrix will be of the following form.

$$\begin{pmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

The eigenvalues of this matrix are $e^{\pm i\theta}$ and 1 which are thus also the eigenvalues of $H$. Clearly the two eigenvalues $e^{\pm i\theta}$ determine the rotation angle.

The eigenvector $y’$ of $H$ corresponding to the real-valued eigenvalue 1 satisfies the condition

$$Hy’ = (1)y’$$ $$\implies ARA^{-1}y’ = y’$$ $$\implies ARA^{-1}Ay = Ay$$ $$\implies ARy = Ay$$

For this to be true $Ry = y$ up to scale. This is true only for the point $(0, 0, 1)$, the center of the rotational symmetry (also the eigenvector of $R$ corresponding to the real eigenvalue of $R$). Hence the image of the center of the rotational symmetry is the eigenvector corresponding to the real eigenvalue of $H$.

References

comments powered by Disqus