Introduction to Projective Geometry Solutions 1.3

Please read this introduction first before looking through the solutions. Here’s a quick index to all the problems in this section.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

1. In a plane perspective, if $P^{\prime }$ is the image of $P$, is $P$ the image of $P^{\prime }$?

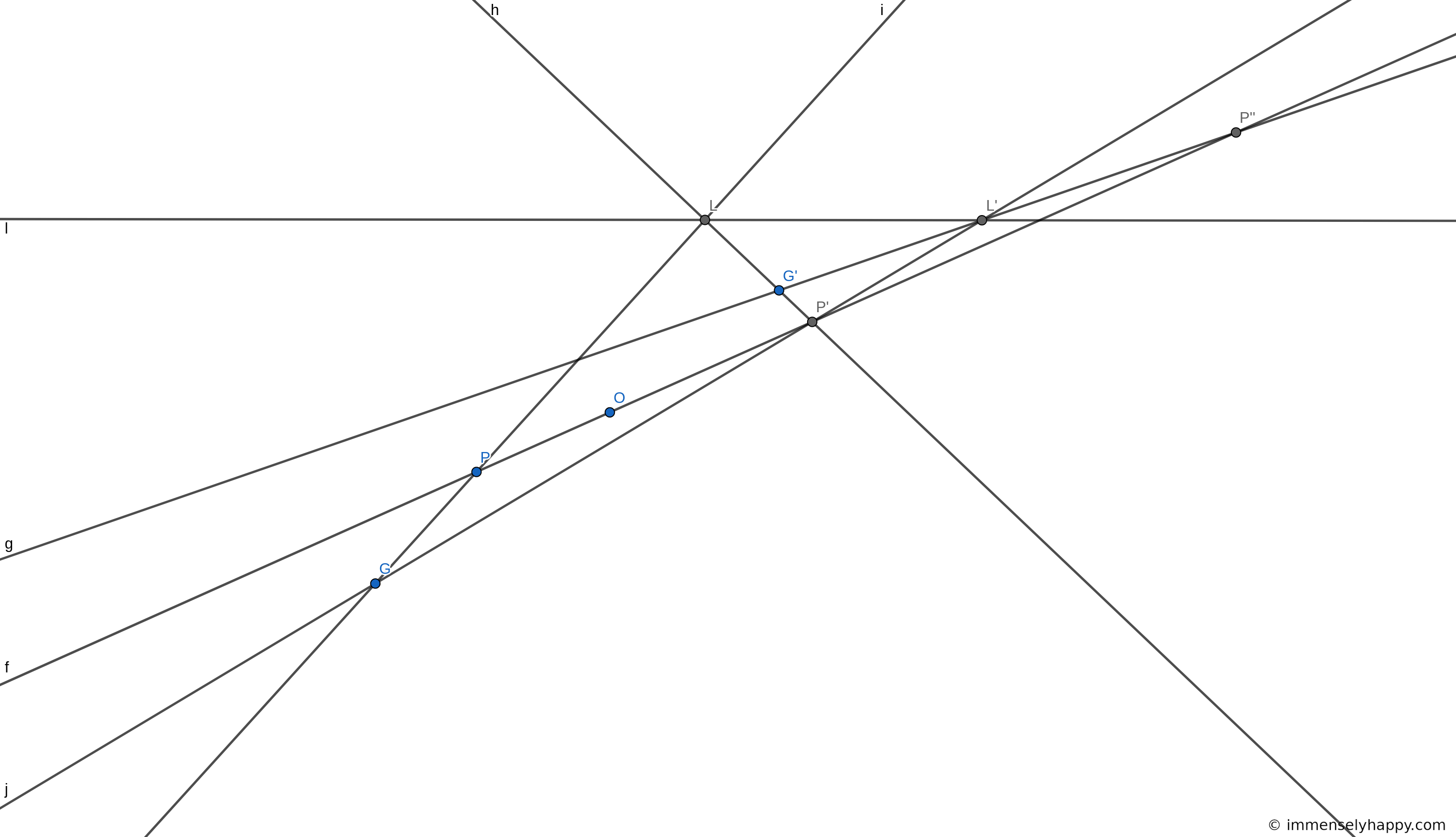
This one is easy to verify by construction. The plane perspective used below is defined by the axis $l$, the center $O$, and the point $G$ along with its image $G^{\prime }$. We can clearly see that $P^{\prime }$ is the image of $P$ which is distinct from the image $P^{\prime \prime }$ of $P^{\prime }$.

An interesting fact that we can observe here is that $P$, $P^{\prime }$ and $P^{\prime \prime }$ are all collinear. Also, note that $O$ functions as the center of perspectivity that establishes a perspective transformation between the lines $PG$ and $P^{\prime }{G}^{\prime }$ and between $P^{\prime }G$ and $P^{\prime }‘G^{\prime }$ thus establishing a projectivity between $PG$ and $P^{\prime }‘G^{\prime }$. Don’t worry if you don’t understand these terms yet; they are explained in detail in the relevant sections 4.4 and 4.5.

2. In a plane perspective, if $G$ and $G^{\prime }$ are distinct points such that each is the image of the other, prove that if $P^{\prime }$ is the image of an arbitrary point $P$, then $P$ is the image of $P^{\prime }$?

As we’ll later learn, this kind of periodic transformation where the image of a point is its preimage is called an involution.

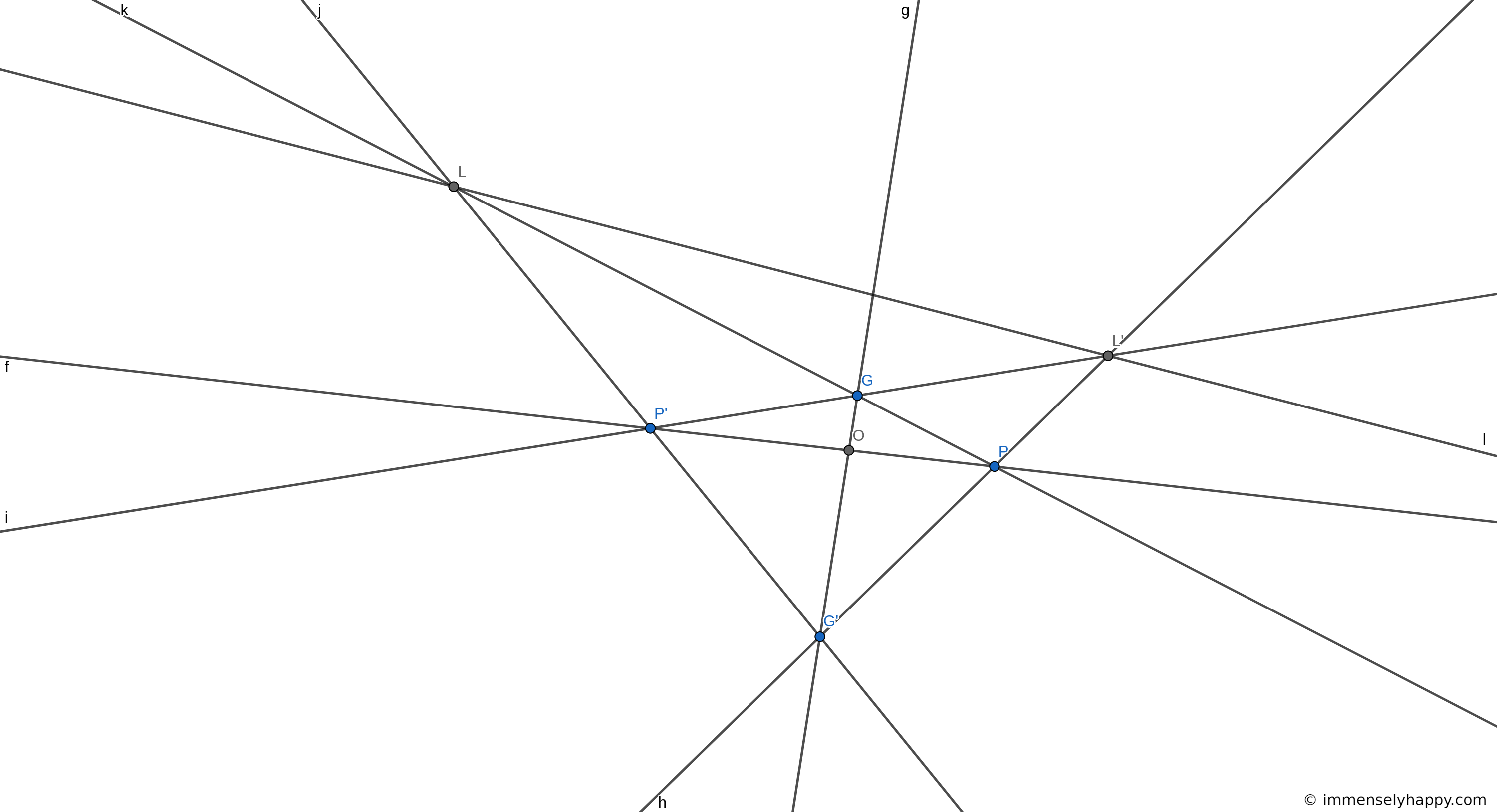
To find the image of $P$, let’s follow the usual procedure. First, we find the intersection, $L$, of $PG$ and the axis $l$. Then we find the intersection of $L{G}^{\prime }$ with $OP$. This is the image $P^{\prime }$ of $P$. As $G$ is the image of $G^{\prime }$, we can also choose $G^{\prime }$ as the starting point instead of $G$. In this case, we’ll first find the intersection, $L^{\prime }$, of $P{G}^{\prime }$ and the axis $l$. Then we’ll find the intersection of $L^{\prime }G$ with $OP$. This means that $P^{\prime }$, the image of $P$, must lie on both $L^{\prime }G$ and $L{G}^{\prime }$. So $P^{\prime }$ is the point of intersection of $L{G}^{\prime }$ and $L^{\prime }G$ and $OP$, $L{G}^{\prime }$ and $L^{\prime }G$ must be concurrent.

To find the image of $P^{\prime }$, we’ll again follow the same two-pronged procedure as outlined above to find that $P^{\prime \prime }$, the image of $P^{\prime }$, must lie on the intersection of $LG$ and $L^{\prime }{G}^{\prime }$. But this point is $P$ by construction! So, the image of $P^{\prime }$ under this transformation is its preimage $P$.

3. Show how to construct the line in the object plane into which the vanishing line in the picture plane is rotated. What is the preimage of this line in the transformation in the object plane?

My solution to this one is a bit different from the one in the book. It’s a bit more inefficient but I kinda like it!

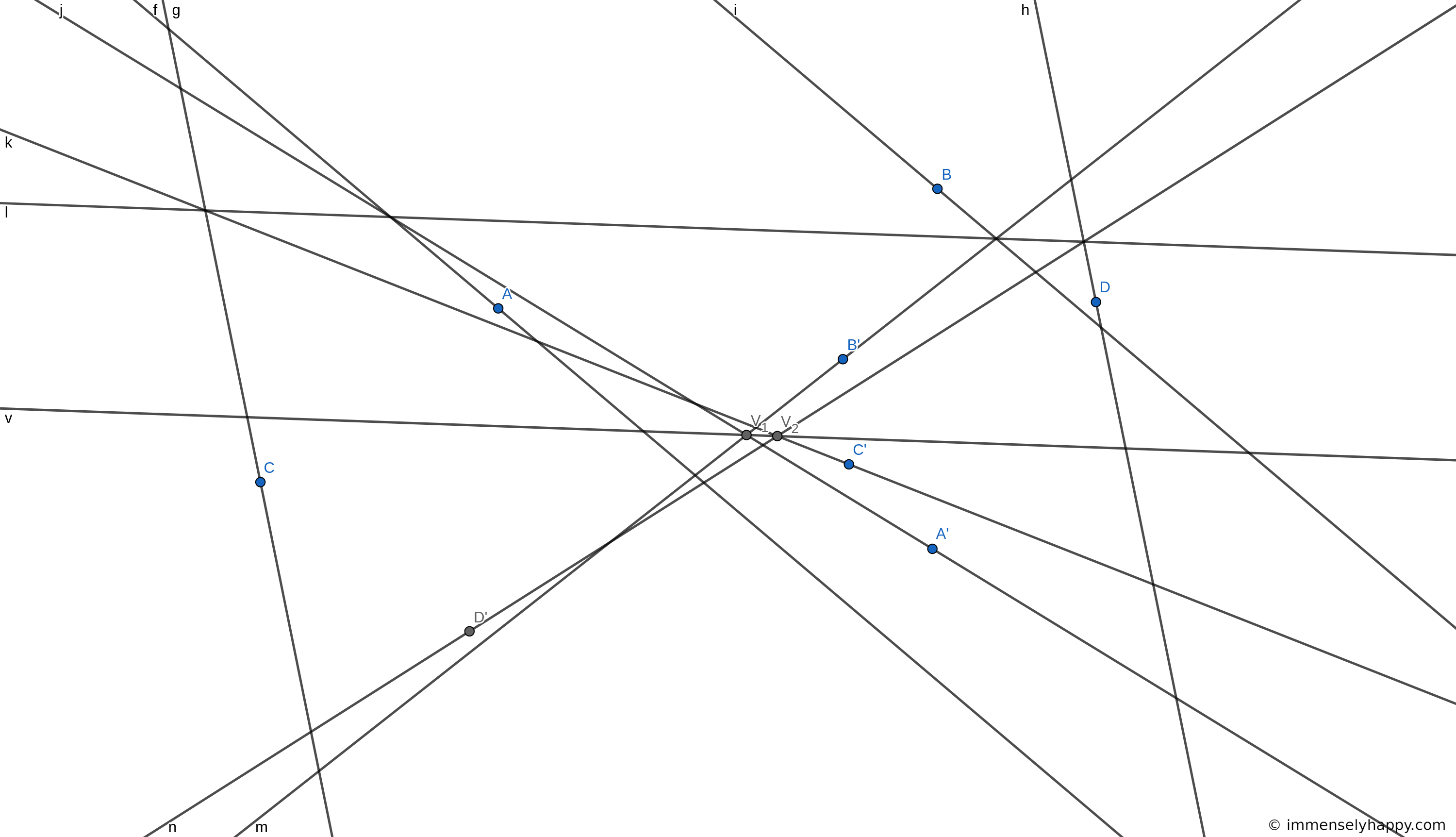
We know that the vanishing line is the locus of the intersections of the images of parallel lines on the object plane. So, if we can find at least two points of intersection of the images of two families of parallel lines then we can construct the line in the object plane onto which the vanishing line in the picture plane is rotated.

We need at least 2 lines from each family of parallel lines to find the points of intersections of their images. So we’ll need 4 pairs of points $A$, $B$, $C$, $D$ and their images $A^{\prime }$, $B^{\prime }$, $C^{\prime }$, $D^{\prime }$. Let’s draw parallel lines from a family through $A$ and $B$ and parallel lines from a different family through $C$ and $D$. Let these lines intersect the axis $l$ at $L_A$, $L_B$, $L_C$, $L_D$. The images of these lines must then be $L_A{A}^{\prime }$, $L_B{B}^{\prime }$, $L_C{C}^{\prime }$, $L_D{D}^{\prime }$. Let the point of intersection of $L_A{A}^{\prime }$, $L_B{B}^{\prime }$ be $V_1$ and of $L_C{C}^{\prime }$, $L_D{D}^{\prime }$ be $V_2$. Then the line through $V_1$ and $V_2$ is the line onto which the vanishing line in the picture plane is rotated.

The answer in the book utilizes the property that the vanishing line is parallel to the axis of the plane perspective. So it needs 4 less points to construct the vanishing line. As you can see from the image below, the vanishing line $v$ is indeed parallel to the axis $l$.

The points of the vanishing line represent the nonexistent points in the object plane to which parallel lines in the object plane appear to converge. Hence this line will have a nonexistent preimage. Talk about an oxymoron!

4. Under what conditions, if any, can a plane perspective be defined by specifying the axis, $l$, and the images, $G^{\prime }$ and $H^{\prime }$, of two points, $G$ and $H$, neither of which is on $l$?

We know that a plane perspective is defined if we are give the following three things.

1. The axis of transformation
2. At least one point (not on the axis) and its image
3. The center of transformation

We have been given the first two and if we can also get the center of transformation from the given information we can define a plane perspective.

The center of transformation lies on the lines between every point and its image. So it will lie on the point of intersection of $G{G}^{\prime }$ and $H{H}^{\prime }$. This point will be defined only if those two lines actually intersect. Hence, for a plane perspective to be defined in this case, $G{G}^{\prime }$ and $H{H}^{\prime }$ must not be parallel.

5. Is a plane perspective determined if one is given the center $O$, and the images, $G^{\prime }$ and $H^{\prime }$, of two noninvariant points, $G$ and $H$?

The solution to this one uses the same technique as for the one above. We’ve been given the center and at least one point and its image. We’ve to find out if we can determine the axis that uniquely determines the plane perspective.

A line and its image intersect at the axis of a plane perspective. So any line through the intersection of $GH$ and $G^{\prime }{H}^{\prime }$, not passing through $C$, can function as the axis of a plane perspective, with $O$ as the center and $G^{\prime }$ and $H^{\prime }$ as images of $G$ and $H$ respectively, provided that those two lines do intersect. Hence the given information is not sufficient to uniquely determine a plane perspective.

Note: If the viewing point $C$ was a point on the axis $l$ then no point would have an image.

6. Show that there is always a plane perspective in which two points, $G$ and $H$, have specified images, $G^{\prime }$ and $H^{\prime }$, unless $G{G}^{\prime }||H{H}^{\prime }$.

To determine a plane perspective in this case, we will need to find out the axis and center of transformation as we’ve been given a point and its image.

Similar to the solution to exercise 4, the center will lie on the intersection of $G{G}^{\prime }$ and $H{H}^{\prime }$. So these two lines must not be parallel. However, there’s no such constraint on $GH$ and $G^{\prime }{H}^{\prime }$.

If $GH$ and $G^{\prime }{H}^{\prime }$ intersect, then similar to the solution to exercise 5, any line through the point of intersection, that doesn’t pass through $O$, can be chosen as the axis and a plane perspective can be determined from this axis, the center and the pair $(G,G^{\prime })$. If they are parallel and do not intersect, the axis can be chosen as any line parallel to $GH$ (and hence $G^{\prime }{H}^{\prime }$), not passing through $O$. Look at the solution to exercise 1.2.10 for a visual explanation.

Hence we can always define a plane perspective given two points and their images such that the lines joining the points and their respective images are not parallel.

7. If $G$, $G^{\prime }$, $H$, $H^{\prime }$, $J$, $J^{\prime }$ are six points such that the lines $G{G}^{\prime }$, $H{H}^{\prime }$, $J{J}^{\prime }$ are concurrent, show that there is a unique plane perspective in which $G^{\prime }$ is the image of $G$, $H^{\prime }$ is the image of $H$, and $J^{\prime }$ is the image of $J$.

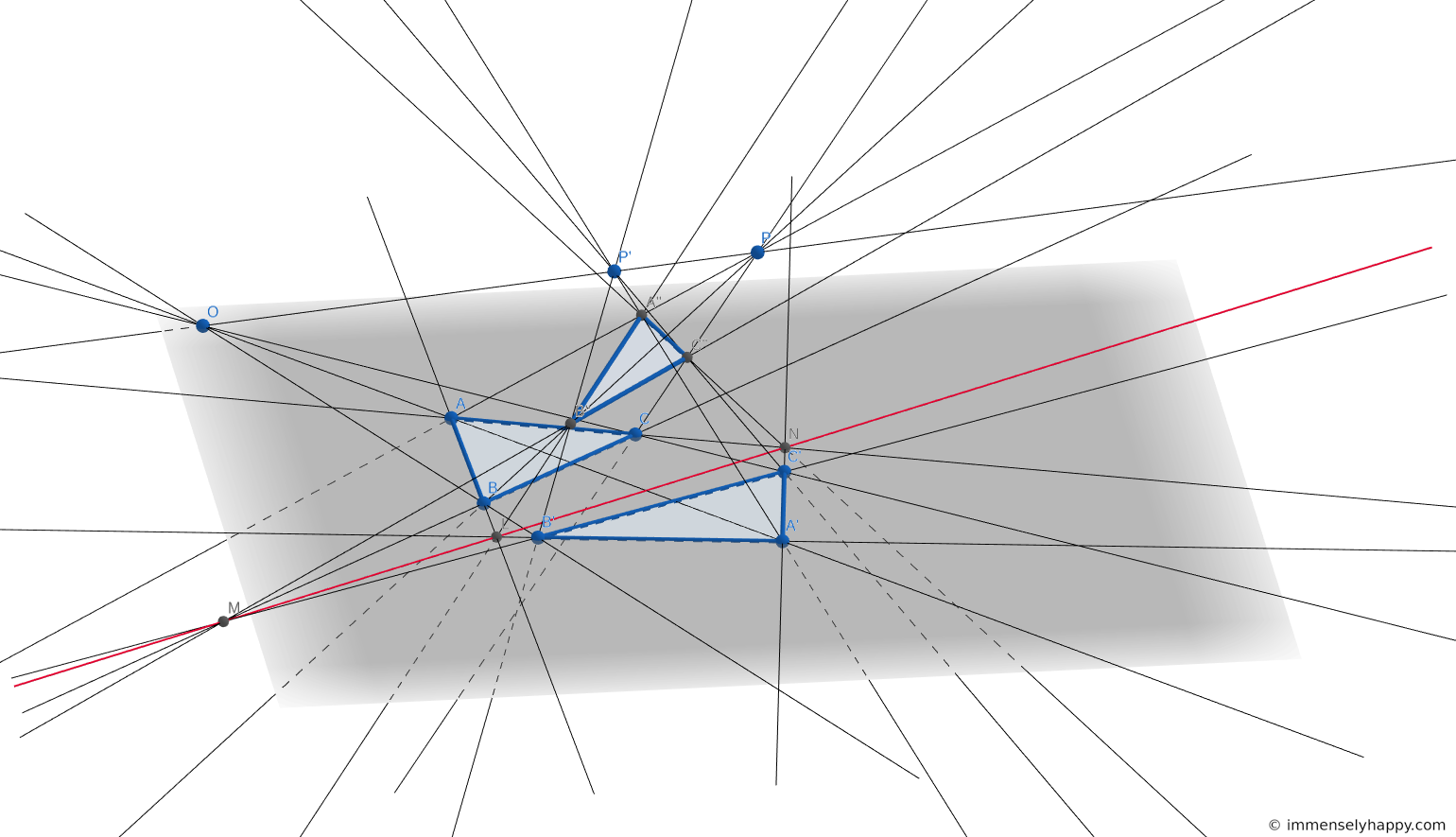
Rephrasing the problem, we need to prove that if $G{G}^{\prime }$, $H{H}^{\prime }$ and $J{J}^{\prime }$ are concurrent then the intersections of the pairs of lines $(GH,G^{\prime }{H}^{\prime })$, $(GJ,G^{\prime }{J}^{\prime })$, $(HJ,H^{\prime }{J}^{\prime })$ are collinear. The point of concurrency will be the center and the line of collinearity will be the axis of the unique plane perspective in which $G^{\prime }$ is the image of $G$, $H^{\prime }$ is the image of $H$, and $J^{\prime }$ is the image of $J$.

The solution to this basically requires you to prove Desargues' theorem.

I wasn’t able to solve this problem on my own because I kept trying to prove it on the 2D plane. From what I understand, no such proof exists; it can only be proven in a 3D plane. This theorem is proved using algebra in a later part of the book (Section 4.3) but here the author is asking for a geometric proof.

As the proof for this theorem has been explained by many others, I don’t want to simply rewrite it just for the sake of completeness. The contribution of this post will be to lead you to a good quality proof instead of poor or mediocre ones, full of holes, some of which that don’t even go through the coplanar case, that I found on the first page of google search results. Here is an excellent proof of Desargues' theorem.

Baker’s Version of Desargues' Theorem

In our case the two triangles will be $GHJ$ and $G^{\prime }{H}^{\prime }{J}^{\prime }$. We’re more interested in the case when the two triangles are coplanar (case 2). Though the proof uses simple plane-plane, plane-line and line-line intersections to prove this theorem, it is fairly involved and needs you to keep a lot of information in your head at the same time. You might have to read this one multiple times for it to sink in.

I’ve made an interactive geogebra version of the diagram given in the proof above so that you can interact with it if you want to. I’ve kept the naming convention used in the proof to make it easier to understand.

8. Using the results of Exercise 7, prove the following theorem. If two triangles are so related that the lines joining corresponding vertices are concurrent, then the intersections of corresponding sides of the two triangles are collinear. (This important result is known as Desargues' theorem).

On the note of Desargues' theorem, I would like to mention a few facts about Desargues himself.

1. Very little is known about him ¹.
2. He is considered to be one of the founders of projective geometry ².
3. He became famous posthumously after another mathematician, Michel Chasles, read his work by chance ³.

What I most liked about him was his practical nature; he tried his best to write about his discoveries in the vernacular.

For the proof look at the solution to the previous exercise.

9. Let a plane perspective in the $xy$ plane be defined by the axis $l:y=0$, the center $O:(0,2)$, the point $G:(1,1)$ and its image $G^{\prime }:(3,-1)$. If $P:(a,b)$ is an arbitrary point, what are the coordinates of its image? What is the vanishing line of this transformation?

Let’s follow the algorithm to construct the image of a general point $P$ not on $G{G}^{\prime }$.

1. Find the equation of the line $PG$ $$\frac{x-1}{a-1}=\frac{y-1}{b-1}$$
2. Find the intersection of $PG$ with the axis $l$. Let’s call this point $L$.
   Setting $y=0$ in the previous equation we get. $$\frac{x-1}{a-1}=\frac{-1}{b-1}$$ $$⟹L=(\frac{b-a}{b-1},0)$$
3. Find the equation of the line $L{G}^{\prime }$. $$\frac{x-3}{\frac{b-a}{b-1}-3}=\frac{y+1}{1}$$ $$⟹x=\frac{y(3-2b-a)+b-a}{b-1}$$
4. Find the equation of the line $OP$. $$\frac{x-0}{a-0}=\frac{y-2}{b-2}$$ $$⟹x=\frac{a(y-2)}{b-2}$$
5. Find the intersection of $L{G}^{\prime }$ and $OP$. This is the equation for $P^{\prime }$, the image of a general point $P$. $$\frac{a(y-2)}{b-2}=\frac{y(3-2b-a)+b-a}{b-1}$$ $$⟹aby-ay-2ab+2a=-2b^{2}y-aby+7by+2ay-6y+b^2-ab-2b+2a$$ $$⟹-2b^{2}y-2aby+7by+3ay-6y+b^2+ab-2b=0$$ $$⟹(-2b^2-2ab+7b+3a-6)y+b^2+ab-2b=0$$ $$⟹(-2b^2-2ab+7b+3a-6)y+b(b+a-2)=0$$ $$⟹(-2b^2-2ab+4b+3b+3a-6)y+b(b+a-2)=0$$ $$⟹(-2b(b+a-2)+3(b+3a-2\left)\right)y+b(b+a-2)=0$$ $$⟹(3-2b)(b+a-2)y+b(b+a-2)=0$$ $$⟹\left(\right(3-2b)y+b)(b+a-2)=0$$ If $b+a-2=0$, then $P$ will be on $G{G}^{\prime }$ which is contradictory to our initial assumption. So the other term must be zero. $$⟹y=\frac{b}{2b-3}$$ To solve for x, we have two equations. $$x=\frac{a(\frac{b}{2b-3}-2)}{b-2}$$ $$⟹\left(\right(2b-3)x+3a)(b-2)=0$$ and $$x=\frac{\frac{b}{2b-3}(3-2b-a)+b-a}{b-1}$$ $$⟹\left(\right(2b-3)x+3a)(b-1)=0$$ For both of these to hold true simultaneously, the common term in both the equations must be zero. Hence $$x=\frac{-3a}{2b-3}$$ and, $$P^{\prime }=(\frac{-3a}{2b-3},\frac{b}{2b-3}),2b-3\ne 0$$

The image of P will not exist if $2b-3=0$. Hence the vanishing line (line that has no image) is the range of points where $b=\frac{3}{2}$. This is the line $y=\frac{3}{2}$.

To construct the image of a point on $G{G}^{\prime }$ we can use the same algorithm but with a point not on $G{G}^{\prime }$, say H, and its image $H^{\prime }$, as calculated from the formula above. If you go through the calculations, you will find the formula of its image to be the same as the one we derived.

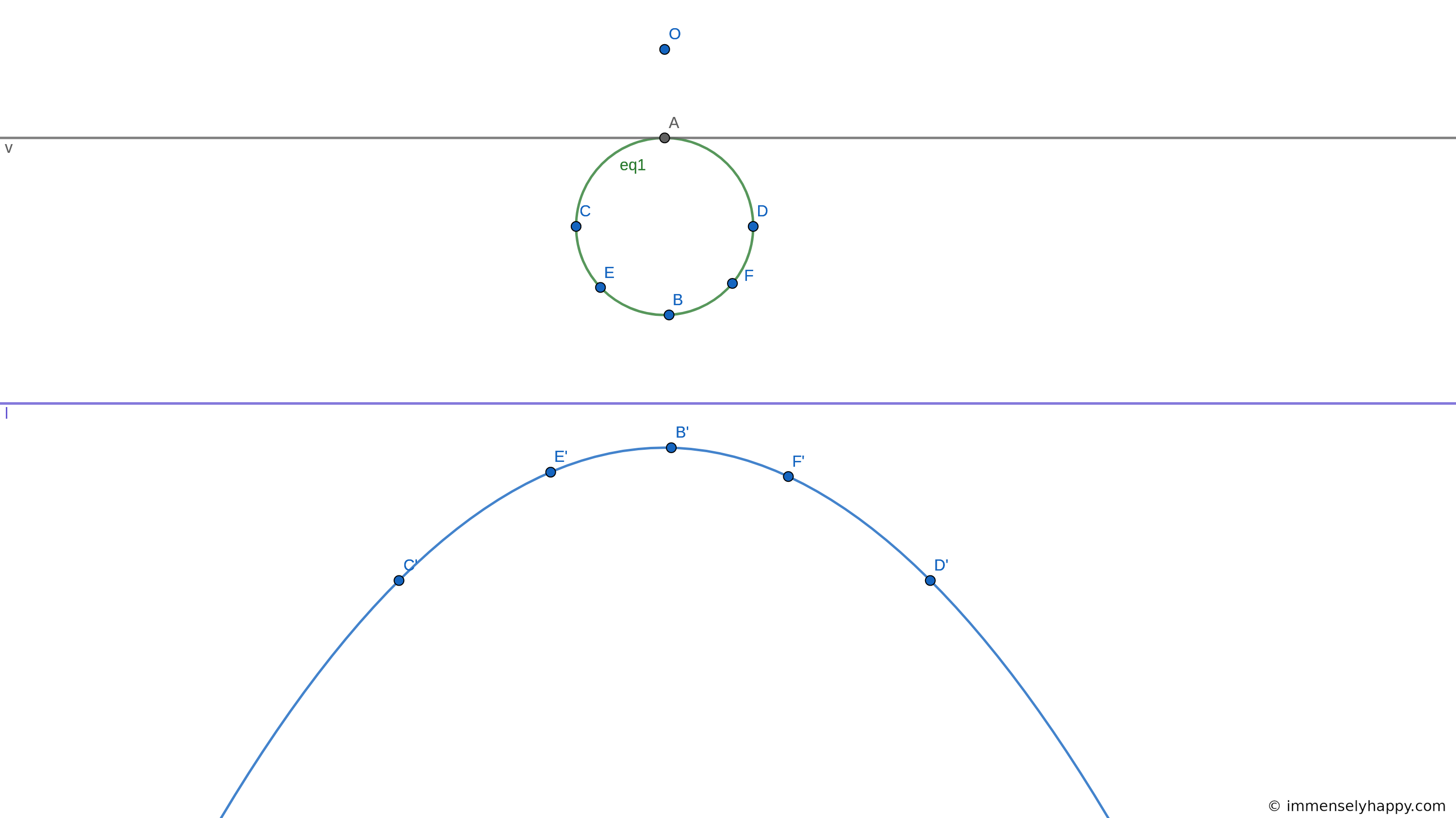
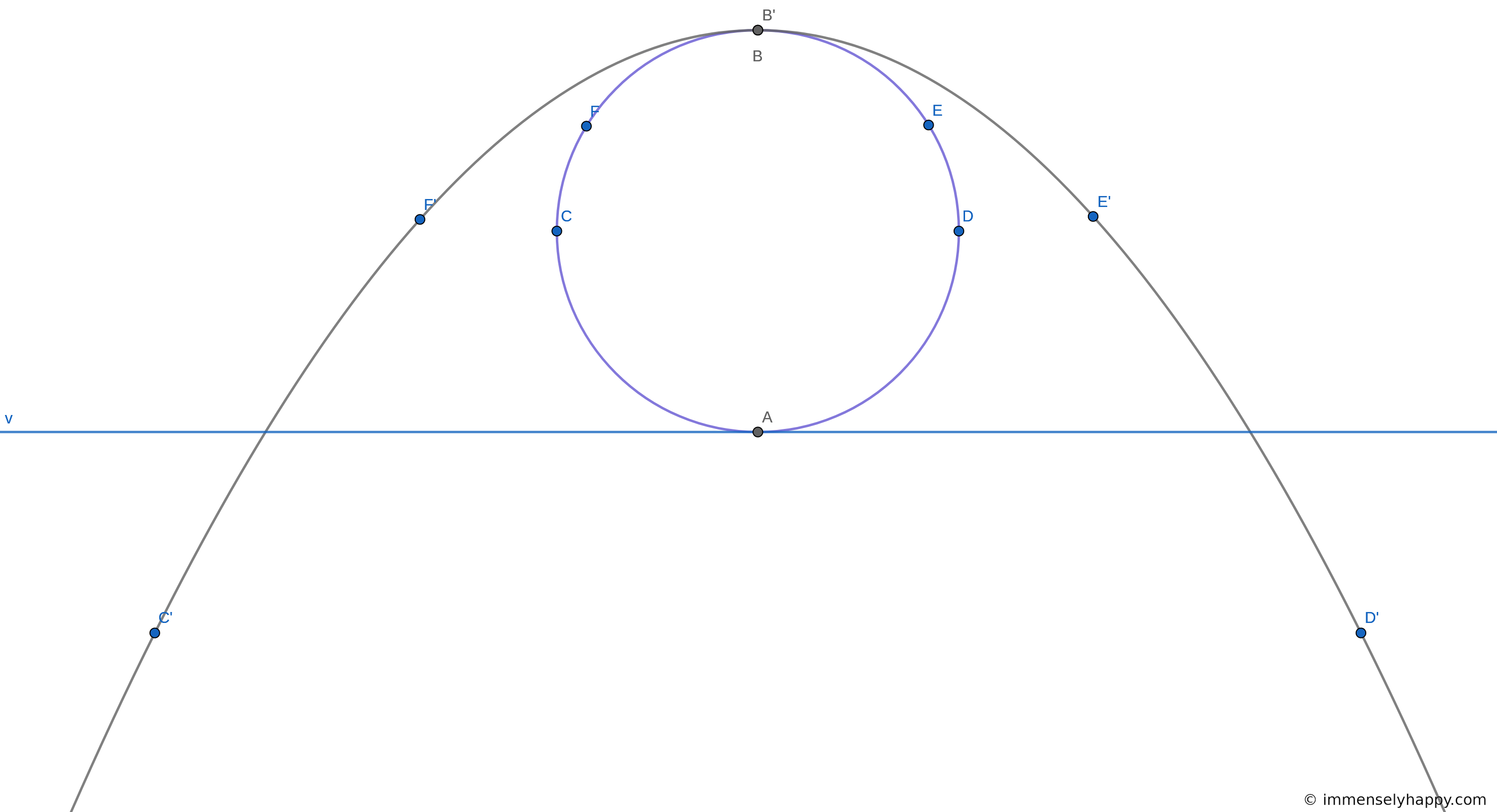
10. In Exercise 9, carry out a point-by-point construction of the image of the circle $x^2+y^2=1$, the circle $x^2+(y-1{)}^2=\frac{1}{4}$, the circle $x^2+(y-1{)}^2=1$.

You only need 5 points to determine a conic section so I guess you could try the point-by-point construction. But I’m going to go with inverting the given equations to find the equations of their images. It’s just more fun for me that way. We can later verify if our construction is correct using the 5 point method.

First, let’s express the object coordinates $(a,b)$ in terms of the image coordinates $(a^{\prime },b^{\prime })$. We know that $$a^{\prime }=\frac{-3a}{2b-3},2b-3\ne 0$$ $$b^{\prime }=\frac{b}{2b-3},2b-3\ne 0.$$ So, $$a=\frac{-a^{\prime }}{2b^{\prime }-1},2b^{\prime }-1\ne 0$$ $$b=\frac{3b^{\prime }}{2b^{\prime }-1},2b^{\prime }-1\ne 0.$$

Note that $y=\frac{1}{2}$ is the vanishing line of the picture plane (line with no preimage).

So, the equation $x^2+y^2=1$ will become $$(\frac{-a^{\prime }}{2b^{\prime }-1}{)}^2+(\frac{3b^{\prime }}{2b^{\prime }-1}{)}^2=1$$ $$⟹a^{\prime 2}+9b^{\prime 2}-4b^{\prime 2}-1+4b^{\prime }=0$$ $$⟹a^{\prime 2}+5b^{\prime 2}+4b^{\prime }-1=0$$

This is the equation of an ellipse. Note that that although the point $B$ looks to be invariant, it is not; it is actually the point that $A$ is mapped to during the transformation. The images of $A$ and $B$ are flipped in the ellipse relative to the original circle. The points $E$ and $D$ are invariant as they lie on the axis $y=0$.

The equation $x^2+(y-1{)}^2=\frac{1}{4}$ will become $$(\frac{-a^{\prime }}{2b^{\prime }-1}{)}^2+(\frac{3b^{\prime }}{2b^{\prime }-1}-1{)}^2=\frac{1}{4}$$ $$⟹4a^{\prime 2}+4(b^{\prime }+1{)}^2-4b^{\prime 2}-1+4b^{\prime }=0$$ $$⟹4a^{\prime 2}+4b^{\prime 2}+4+8b^{\prime }-4b^{\prime 2}-1+4b^{\prime }=0$$ $$⟹4a^{\prime 2}+12b^{\prime }+3=0$$

This is the equation of a parabola. Note that the vanishing line $y=\frac{3}{2}$ is tangent to the original circle at $A(0,\frac{3}{2})$. So $A$ does not have an image.

The last equation $x^2+(y-1{)}^2=1$ will become $$(\frac{-a^{\prime }}{2b^{\prime }-1}{)}^2+(\frac{3b^{\prime }}{2b^{\prime }-1}-1{)}^2=1$$ $$⟹a^{\prime 2}+(b^{\prime }+1{)}^2-4b^{\prime 2}-1+4b^{\prime }=0$$ $$⟹a^{\prime 2}+b^{\prime 2}+1+2b^{\prime }-4b^{\prime 2}-1+4b^{\prime }=0$$ $$⟹a^{\prime 2}-3b^{\prime 2}+6b^{\prime }=0$$

This is the equation of a hyperbola. Note that the vanishing line $y=\frac{3}{2}$ intersects with the original circle at two points $(\pm \frac{\sqrt{3}}{2},\frac{3}{2})$ which hence don’t have images. Also note that the points $O$ and $E$ on the circle are invariant, the first is the center of the plane perspective and the second lies on the axis.

11. Work Exercise 9 if the axis is the line $y=x$, the center is the point $(1,0)$, $G$ is the point $(-1,0)$, and $G^{\prime }$ is the point $(-2,0)$.

Let’s follow the same 4-step procedure as in #9 to find the image of a general point $P$ not on $G{G}^{\prime }$.

1. Find the equation of the line $PG$ $$\frac{x+1}{a+1}=\frac{y}{b}$$
2. Find the intersection of $PG$ with the axis $l$. Let’s call this point $L$.
   Setting $y=x$ in the previous equation we get. $$\frac{x+1}{a+1}=\frac{x}{b}$$ $$⟹L=(\frac{b}{a+1-b},\frac{b}{a+1-b})$$
3. Find the equation of the line $L{G}^{\prime }$. $$\frac{x+2}{\frac{b}{a+1-b}+2}=\frac{y}{\frac{b}{a+1-b}}$$ $$⟹b(x+2)=by+2(1+a-b)y$$ $$⟹bx+2b=by+2y+2ay-2by$$ $$⟹bx+2b=2y+2ay-by$$ $$⟹y=\frac{bx+2b}{2+2a-b}$$
4. Find the equation of the line $OP$. $$\frac{x-1}{a-1}=\frac{y}{b}$$ $$⟹y=\frac{b(x-1)}{a-1}$$
5. Find the intersection of $L{G}^{\prime }$ and $OP$. This is the equation for $P^{\prime }$, the image of a general point $P$. $$\frac{bx+2b}{2+2a-b}=\frac{b(x-1)}{a-1}$$ As $b\ne 0$ (else $P$ would be on $G{G}^{\prime }$ which is contradictory to our initial assumption), $$\frac{x+2}{2+2a-b}=\frac{x-1}{a-1}$$ $$⟹(x+2)(a-1)=(x-1)(2+2a-b)$$ $$⟹ax+2a-x-2=2x-2+2ax-2a-bx+b$$ $$⟹3x+ax-4a-bx+b=0$$ $$⟹x=\frac{4a-b}{a+3-b}$$ To solve for y, we have two equations. $$y=\frac{\frac{b(4a-b)}{a+3-b}+2b}{2+2a-b}$$ $$⟹\left(\right(a+3-b)y-3b)(2a-b+2)=0$$ and $$y=\frac{b\left(\right(\frac{4a-b}{a+3-b})-1)}{a-1}$$ $$⟹\left(\right(a+3-b)y-3b)(a-1)=0$$ For both of these to hold true simultaneously, the common term in both the equations must be zero. Hence $$y=\frac{3b}{a+3-b}$$ and, $$P^{\prime }=(\frac{4a-b}{a+3-b},\frac{3b}{a+3-b}),a+3-b\ne 0$$

The image of P will not exist if $a+3-b=0$. Hence the vanishing line (line that has no image) is the range of points where $a+3-b=0$. This is the line $x-y+3=0$.

To construct the image of a point on $G{G}^{\prime }$ we can use the same algorithm but with a point not on $G{G}^{\prime }$, say H, and its image $H^{\prime }$, as calculated from the formula above. If you go through the calculations, you will find the formula of its image to be the same as the one we derived.

12. Work Exercise 9 if the axis is the line $x+y=0$, the center is the point $(1,1)$, $G$ is the point $(-1,-1)$, and $G^{\prime }$ is the point $(2,2)$.

Let’s follow the same 4-step procedure as in #9 to find the image of a general point $P$ not on $G{G}^{\prime }$.

1. Find the equation of the line $PG$ $$\frac{x+1}{a+1}=\frac{y+1}{b+1}$$
2. Find the intersection of $PG$ with the axis $l$. Let’s call this point $L$.
   Setting $y=-x$ in the previous equation we get. $$\frac{x+1}{a+1}=\frac{-x+1}{b+1}$$ $$⟹(x+1)(b+1)=(1-x)(a+1)$$ $$⟹bx+b+x+1=a-ax+1-x$$ $$⟹(b+a+2)x=a-b$$ $$⟹x=\frac{a-b}{a+b+2}$$ $$⟹L=(\frac{a-b}{a+b+2},\frac{b-a}{a+b+2})$$
3. Find the equation of the line $L{G}^{\prime }$. $$\frac{x-2}{\frac{a-b}{a+b+2}-2}=\frac{y-2}{\frac{b-a}{a+b+2}-2}$$ $$⟹(x-2)\left(\frac{-b-3a-4}{a+b+2}\right)=(y-2)\left(\frac{-a-3b-4}{a+b+2}\right)$$ $$⟹(x-2)(-b-3a-4)=(y-2)(-a-3b-4)$$ $$⟹x=\frac{y(a+3b+4)+4(a-b)}{b+3a+4}$$
4. Find the equation of the line $OP$. $$\frac{x-1}{a-1}=\frac{y-1}{b-1}$$ $$⟹x=\frac{y(a-1)+b-a}{b-1}$$
5. Find the intersection of $L{G}^{\prime }$ and $OP$. This is the equation for $P^{\prime }$, the image of a general point $P$. $$\frac{y(a-1)+b-a}{b-1}=\frac{y(a+3b+4)+4(a-b)}{b+3a+4}$$ $$⟹\left(y\right(a-1)+b-a)(b+3a+4)=\left(y\right(a+3b+4)+4(a-b\left)\right)(b-1)$$ $$⟹(3a^2-3b^2+2a-2b)y+5b^2-2ab-3a^2=0$$ $$⟹\left(3\right(a-b\left)\right(a+b)+2(a-b\left)\right)y+5b^2-5ab+3ab-3a^2=0$$ $$⟹(a-b)(3a+3b+2)y+5b(b-a)+3a(b-a)=0$$ $$⟹(a-b)\left(\right(3a+3b+2)y-5b-3a)=0$$ As $a-b\ne 0$ as $P$ does not lie on $G{G}^{\prime }$, we get $$y=\frac{5b+3a}{3b+3a+2}$$ To solve for x, we have two equations. $$x=\frac{\frac{5b+3a}{3b+3a+2}(a+3b+4)+4(a-b)}{b+3a+4}$$ $$x=\frac{3b^2+14ab+12b+15a^2+20a}{(b+3a+4)(3b+3a+2)}$$ $$x=\frac{(b+3a+4)(3b+5a)}{(b+3a+4)(3b+3a+2)}$$ $$(b+3a+4)\left(\right(3b+3a+2)x-3b-5a)=0$$ and, $$x=\frac{\frac{5b+3a}{3b+3a+2}(a-1)+b-a}{b-1}$$ $$x=\frac{3b^2+5ab-3b-5a}{(3b+3a+2)(b-1)}$$ $$x=\frac{(3b+5a)(b-1)}{(3b+3a+2)(b-1)}$$ $$(b-1)\left(\right(3b+3a+2)x-3b-5a)=0$$ For both of these to hold true simultaneously, the common term in both the equations must be zero. Hence $$x=\frac{3b+5a}{3b+3a+2}$$ and, $$P^{\prime }=(\frac{3b+5a}{3b+3a+2},\frac{3a+5b}{3b+3a+2}),3b+3a+2\ne 0$$

The image of P will not exist if $3b+3a+2=0$. Hence the vanishing line (line that has no image) is the range of points where $3b+3a+2=0$. This is the line $3x+3y+2=0$.

To construct the image of a point on $G{G}^{\prime }$ we can use the same algorithm but with a point not on $G{G}^{\prime }$, say H, and its image $H^{\prime }$, as calculated from the formula above. If you go through the calculations, you will find the formula of its image to be the same as the one we derived.

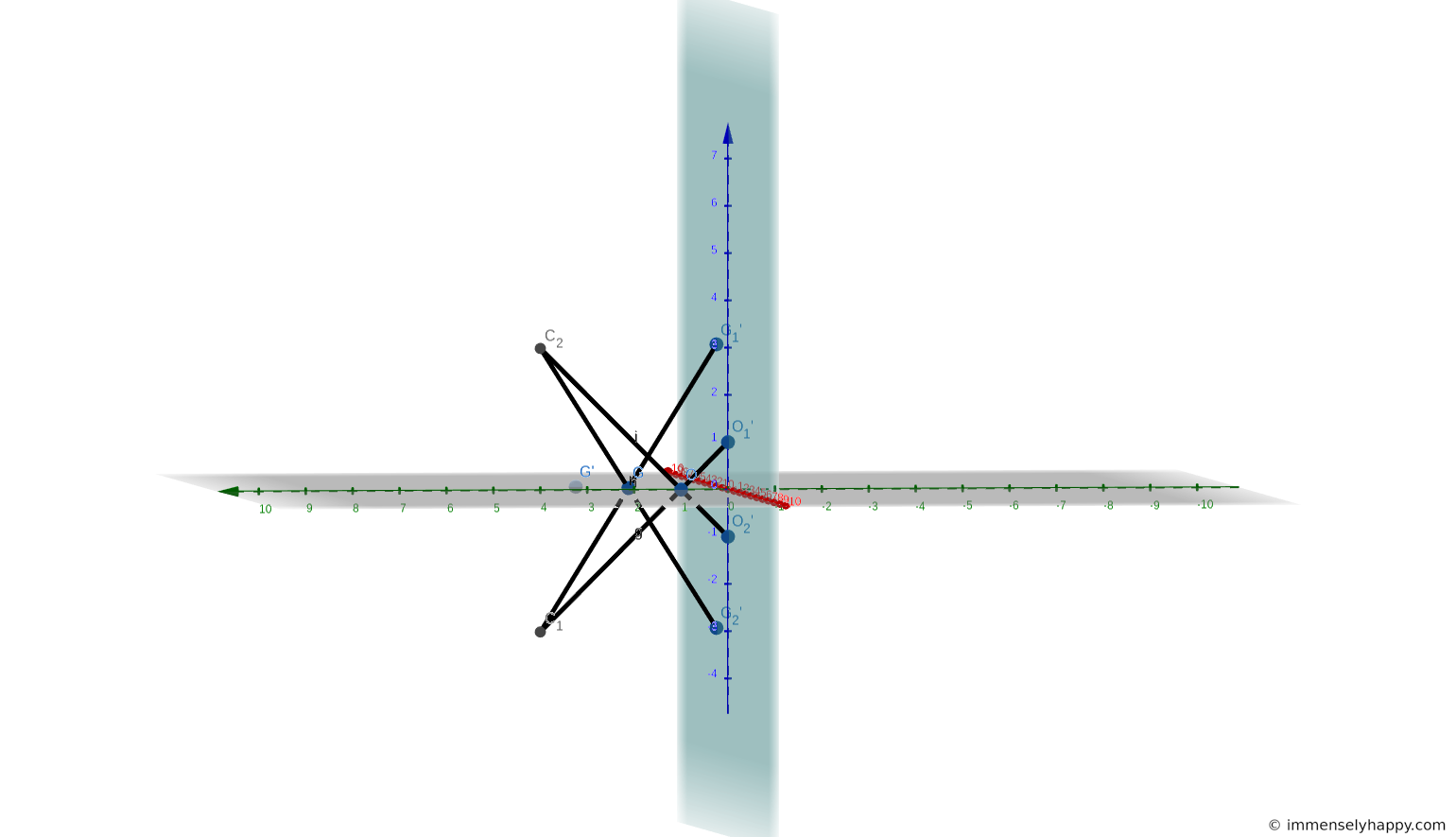
13. In a plane perspective in the $xy$ plane, $O$ is the point $(0,1)$, and $l$ is the $x$ axis. If the image of the point $G:(1,2)$ is the point $G^{\prime }:(2,3)$, what are the coordinates of the viewing point in the equivalent three-dimensional perspective?

If the plane perspective is in the $xy$ plane and the axis is the $x$ axis, the picture plane must be the $xz$ plane as it must be perpendicular to the $xy$ plane and intersect it at the $x$ axis.

As $O$ is invariant, it’s image $O^{\prime }$ on the picture plane must be $O$ rotated by ${90}^{\circ }$ about the $x$ axis. The image of $G$ on the picture plane is $G^{\prime }$ rotated by ${90}^{\circ }$ about the $x$ axis.

The viewing point $C$ must lie at the intersection of the line $O{O}^{\prime }$ and the line $G{G}^{\prime \prime }$.

We haven’t specified which direction to rotate the points in though. Let’s try both clockwise and counter-clockwise and see if we get a valid viewing point.

Clockwise rotation of $xy$ plane with the $z$ axis facing up

The image of $G$ on the picture plane will be $G_1^{\prime }$.

Let’s write down the 3D coordinates of the given points. $$O:(0,1,0)$$ $$O^{\prime }:(0,0,1)$$ $$G:(1,2,0)$$ $$G^{\prime }:(2,3,0)$$ $$G_1^{\prime }:(2,0,3)$$

Here we can’t use the symmetric form of the equation of a line in 3D because the denominator will be zero for the $x$ term. So I’m going to use the parametric form.

$$O{O}^{\prime }=(0,1,0)+t(0,-1,1)$$

$$G{G}_1^{\prime }=(1,2,0)+v(1,-2,3)$$

These two lines will intersect if we can find real values for $t$ and $v$ such that

$$(1,2,0)+v(1,-2,3)=(0,1,0)+t(0,-1,1)$$

If we solve these three equations in two unknowns, we see that the system has a solution and the values for $t$ and $v$ that satisfy this equation are

$$v=-1$$ $$t=-3$$

and $C_1=(0,4,-3)$.

Counter-clockwise rotation of $xy$ plane with the $z$ axis facing up

The image of $G$ on the picture plane will be $G_2^{\prime }$.

Let’s write down the 3D coordinates of the given points. $$O:(0,1,0)$$ $$O^{\prime }:(0,0,-1)$$ $$G:(1,2,0)$$ $$G^{\prime }:(2,3,0)$$ $$G_2^{\prime }:(2,0,-3)$$

$$O{O}^{\prime }=(0,1,0)+t(0,-1,-1)$$

$$G{G}_2^{\prime }=(1,2,0)+v(1,-2,-3)$$

These two lines will intersect if we can find real values for $t$ and $v$ such that

$$(1,2,0)+v(1,-2,-3)=(0,1,0)+t(0,-1,-1)$$

If we solve these three equations in two unknowns, we see that the system has a solution and the values for $t$ and $v$ that satisfy this equation are

$$v=-1$$ $$t=-3$$

and $C_2=(0,4,3)$.

Let’s look at the projections from both the viewing points $C_1$ and $C_2$.

Now according to rules of rabbatement (Page 12), the picture plane is rotated until the half of it facing the viewing point coincides with the half of the object plane on the opposite side of the picture plane from the viewing point.

If we follow the process with $C_2$, then the coordinates of the $G^{\prime }$ and $O$ would have to be $(2,-3,0)$ and $(0,-1,0)$ respectively. However, this is not the case. Hence $C_2$ is not a valid viewing point.

When we follow the process with $C_1$ we get the coordinates of $G^{\prime }$ and $O$ to be $(2,3,0)$ and $(0,1,0)$. Hence, $C_1$ is a valid viewing point and the answer to this exercise.

14. Work exercise 13 if $O$ is the point $(1,2)$, $l$ is still the $x$ axis, and the image of the point $(0,3)$ is the point $(2,1)$.

Let’s follow the same procedure as in #13.

Clockwise rotation of $xy$ plane with the $z$ axis facing up

The image of $G$ on the picture plane will be $G_1^{\prime }$.

Let’s write down the 3D coordinates of the given points. $$O:(1,2,0)$$ $$O^{\prime }:(1,0,2)$$ $$G:(0,3,0)$$ $$G^{\prime }:(2,1,0)$$ $$G_1^{\prime }:(2,0,1)$$

$$O{O}^{\prime }=(1,2,0)+t(0,-2,2)$$

$$G{G}_1^{\prime }=(2,1,0)+v(0,-1,1)$$

As these two lines do not intersect (they are skew lines), there is no viewing point $C$ that can produce this transformation.

Clockwise rotation of $xy$ plane with the $z$ axis facing up

The image of $G$ on the picture plane will be $G_2^{\prime }$.

Let’s write down the 3D coordinates of the given points. $$O:(1,2,0)$$ $$O^{\prime }:(1,0,-2)$$ $$G:(0,3,0)$$ $$G^{\prime }:(2,1,0)$$ $$G_1^{\prime }:(2,0,-1)$$

$$O{O}^{\prime }=(1,2,0)+t(0,-2,-2)$$

$$G{G}_1^{\prime }=(2,1,0)+v(0,-1,-1)$$

Again, as these two lines do not intersect (they are skew lines), there is no viewing point $C$ that can produce this transformation.

Hence, there is no viewing point in 3D that can produce either of the two transformations.

15. In a plane perspective, $l$ is the $x$ axis, $O$ is the point $(0,3)$, and $G$ is the point $(0,1)$. Determine the coordinates of the image of $G$ if the perspective is to have the property that if $P^{\prime }$ is the image of an arbitrary point $P$, the $P$ is the image of $P^{\prime }$.

This is again an involution where applying the transformation twice will give back the point you started with.

We know that the image of a point must lie on the line that passes through the point and the center $O$. This is the line $OG:x=0$ in this case. Hence the coordinates of the image $G^{\prime }$ must have a zero $x$-component. So, we can represent the coordinates of $G^{\prime }$ as $(0,a)$.

The property of the given transformation is that the image of $G(0,1)$ is $G^{\prime }(0,b)$ and the image of $G^{\prime }(0,b)$ is $G(0,1)$. If we consider these points in 3D we’ll get some more information. Let’s call the points on the object plane $P_1$ and $P_2$ and their images on the picture plane as $P_1^{\prime }$ and $P_2^{\prime }$ respectively. Then, we get the following.

$$P_1=(0,1,0)$$ $$P_2=(0,a,0)$$ $$P_1^{\prime }=(0,0,a)$$ $$P_2^{\prime }=(0,0,1)$$ $$O=(0,3,0)$$ $$O^{\prime }=(0,0,3)$$

We know that under a perspective transformation the lines $O{O}^{\prime }$, $P_1{P}_1^{\prime }$ and $P_2{P}_2^{\prime }$ must be concurrent at the viewing point $C$. So we must solve for the variable $a$ such that

$$(0,3,0)+r(0,-3,3)=(0,1,0)+s(0,-1,a)=(0,0,1)+t(0,a,-1).$$

Solving this we get the quadratic equation

$$(a+3)(a-1)=0$$

If $a=1$, then $G$ is its own image; but this is not possible as $G$ does not lie on the axis of the plane perspective. So $a$ must be $-3$ and G' = (0, -3) is the image of $G$ with the property that $G$ is the image of $G^{\prime }$ under the given transformation.

16. Given two intersecting lines, show how to determine a plane perspective which will transform them into parallel lines.

We know that the image of parallel lines converge at the vanishing line of the plane perspective. Working backwards, any line through the intersection of the two given lines if taken as the vanishing line $v$ will determine a plane perspective that transforms them into parallel lines (or rather transforms the parallel lines into the given converging lines, it can go both ways). Any point $O$, not on the vanishing line, can serve as the center and any line parallel to the vanishing line not passing through $O$ can serve as the axis $l$ of the plane perspective. Both lines will be parallel to $OV$, where $V$ is the point of convergence of the two given lines.

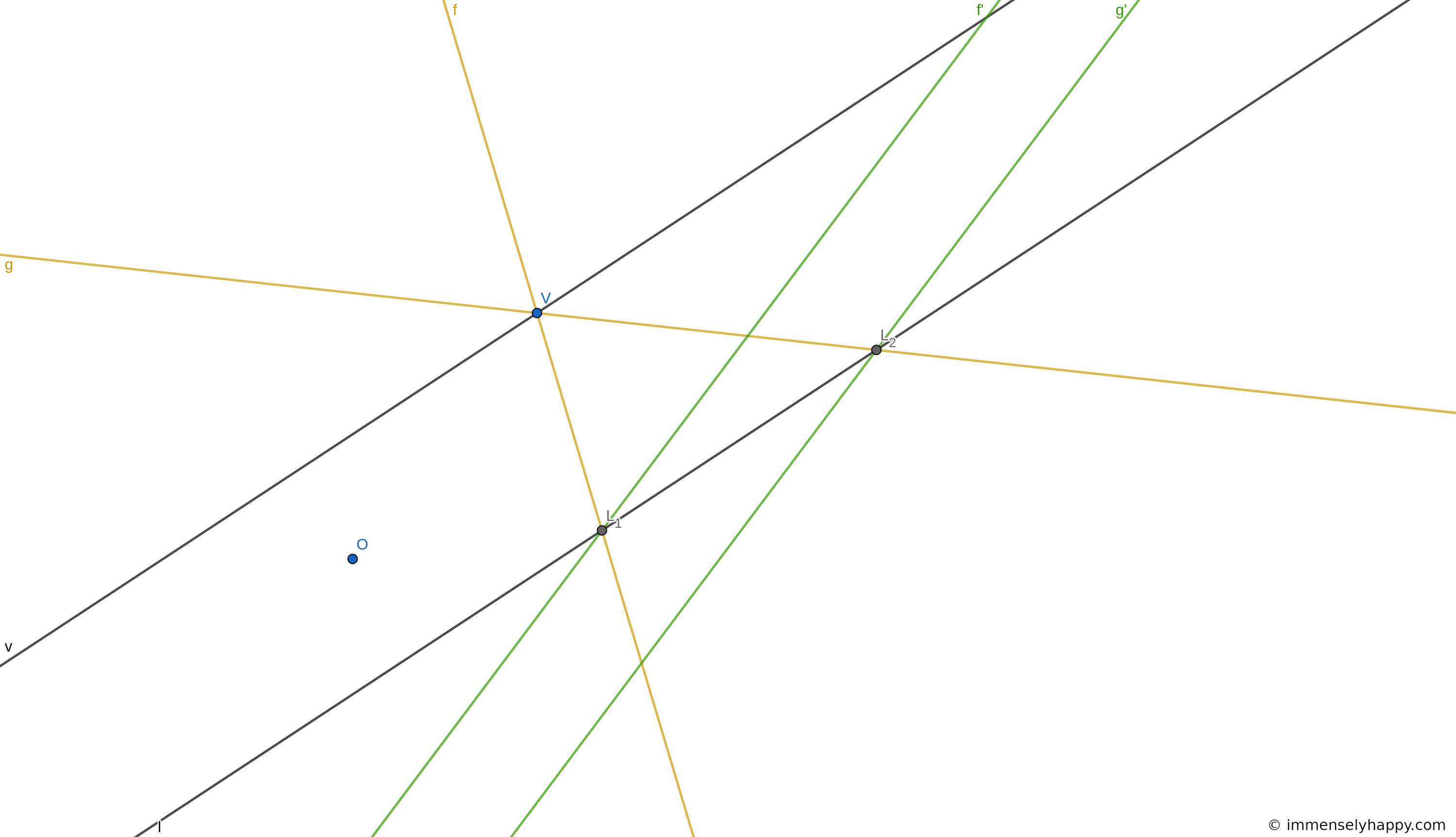
17. Given the center, $C$, the vanishing line, $v$, a point $G$ and its image $G^{\prime }$ in a plane perspective, show how to construct the axis of the perspective.

Here are the steps to construct the axis of a plane perspective with the given information.

1. Draw any line $\rho$ not parallel to $v$ through $G$ which intersects $v$ at $V$.
2. Draw the line parallel to $CV$ that passes through $G^{\prime }$. This is the image ${\rho }^{\prime }$ of $\rho$ by Theorem 1.
3. The line parallel to $v$ through the point of intersection of $\rho$ and ${\rho }^{\prime }$ is the axis $l$ of the given plane perspective (see derivation of vanishing line on Page 14).

18. Prove that a plane perspective is uniquely determined when its center, its vanishing line, and the image $G^{\prime }$, of one point, $G$, are given.

As we can derive the axis of the plane perspective from the given information using the steps outlined in #17, we have all the information required to uniquely determine a plane perspective, i.e. the axis, the center and a point and its image.

19. Work Exercise 9 if $l$ is the vanishing line of the plane perspective instead of its axis.

Following is the algorithm to find the image of a general point $P(a,b)$ using the given information.

1. Find the equation of the line $PG$ $$\frac{x-1}{a-1}=\frac{y-1}{b-1}$$
2. Find the intersection of $PG$ with the vanishing line $v$. Let’s call this point $V$.
   Setting $y=0$ in the previous equation we get. $$\frac{x-1}{a-1}=\frac{-1}{b-1}$$ $$⟹V=(\frac{b-a}{b-1},0)$$
3. Find the slope of the line $OV$. $$slope=\frac{2-0}{0-\frac{b-a}{b-1}}$$ $$⟹slope=\frac{2(1-b)}{b-a}$$
4. Find the equation of the line through G' parallel to $OV$. By Theorem 1, this is the image of the line $PG$. $$\frac{y+1}{x-3}=\frac{2(1-b)}{b-a}$$ $$⟹x=\frac{(b-a)y-5b-a+6}{2(1-b)}$$
5. Find the equation of the line $OP$. $$\frac{x-0}{a-0}=\frac{y-2}{b-2}$$ $$⟹x=\frac{a(y-2)}{b-2}$$
6. Find the intersection of the line from step 4 with $OP$. This will be $P^{\prime }$, the image of $P$. $$\frac{(b-a)y-5b-a+6}{2(1-b)}=\frac{a(y-2)}{b-2}$$ $$⟹b^{2}y+aby-2by-5b^2-5ab+16b+6a-12=0$$ $$⟹(b^2+ab-2b)y-5b^2-5ab+10b+6b+6a-12=0$$ $$⟹by(b+a-2)-5b(b+a-2)+6(b+a-2)=0$$ $$⟹(by-5b+6)(b+a-2)=0$$ $a+b-2\ne 0$, as P is not on GG'. So we get $$by-5b+6=0$$ $$⟹y=\frac{5b-6}{b}$$ To solve for x, we have two equations. $$x=\frac{a(\frac{5b-6}{b}-2)}{b-2}$$ $$⟹x=\frac{3a(b-2)}{\left(b\right)(b-2)}$$ $$⟹(b-2)(bx-3a)=0$$ and, $$x=\frac{(b-a)\left(\frac{5b-6}{b}\right)-5b-a+6}{2(1-b)}$$ $$⟹x=\frac{3a(b-1)}{(1-b)\left(b\right)}$$ $$⟹(bx-3a)(1-b)=0$$ For both of these to hold true simultaneously, the common term in both the equations must be zero. Hence $$x=\frac{3a}{b}$$ and, $$P^{\prime }=(\frac{3a}{b},\frac{5b-6}{b}),b\ne 0$$

Note that we already know $y=0$ to be the vanishing line in this case.

20. In Exercise 9, if $l$ is the vanishing line instead of the axis, carry out a point-by-point construction of the image of the circle $x^2+y^2=1$, the circle $x^2+(y-1{)}^2=\frac{1}{4}$, the circle $x^2+(y-1{)}^2=1$.

First, let’s express the object coordinates $(a,b)$ in terms of the image coordinates $(a^{\prime },b^{\prime })$. We know that $$a^{\prime }=\frac{3a}{b},b\ne 0$$ $$b^{\prime }=\frac{5b-6}{b},b\ne 0$$ So, $$a=\frac{2a^{\prime }}{5-b^{\prime }},b^{\prime }\ne 5$$ $$b=\frac{6}{5-b^{\prime }},b^{\prime }\ne 5$$

Note that $y=5$ is the vanishing line of the picture plane (line with no preimage).

So, the equation $x^2+y^2=1$ will become $$(\frac{2a^{\prime }}{5-b^{\prime }}{)}^2+(\frac{6}{5-b^{\prime }}{)}^2=1$$ $$4a^{\prime 2}+36-25-b^{\prime 2}+10b^{\prime }=0$$ $$4a^{\prime 2}-b^{\prime 2}+10b^{\prime }+11=0$$

This is the equation of a hyperbola. Note that the vanishing line $y=0$ intersects with the original circle at two points $(\pm 1,0)$ which hence don’t have images.

The equation $x^2+(y-1{)}^2=\frac{1}{4}$ will become $$(\frac{2a^{\prime }}{5-b^{\prime }}{)}^2+(\frac{6}{5-b^{\prime }}-1{)}^2=\frac{1}{4}$$ $$16a^{\prime 2}+4(1+b^{\prime }{)}^2-(5-b^{\prime }{)}^2=0$$ $$16a^{\prime 2}+4+4b^{\prime 2}+8b^{\prime }-25-b^{\prime 2}+10b^{\prime }=0$$ $$16a^{\prime 2}+3b^{\prime 2}+18b^{\prime }-21=0$$

This is the equation of an ellipse.

The last equation $x^2+(y-1{)}^2=1$ will become $$(\frac{2a^{\prime }}{5-b^{\prime }}{)}^2+(\frac{6}{5-b^{\prime }}-1{)}^2=1$$ $$4a^{\prime 2}+(1+b^{\prime }{)}^2-(5-b^{\prime }{)}^2=0$$ $$4a^{\prime 2}+1+b^{\prime 2}+2b^{\prime }-25-b^{\prime 2}+10b^{\prime }=0$$ $$4a^{\prime 2}-24+12b^{\prime }=0$$

This is the equation of a parabola. Note that point at which the vanishing line is tangent to the original circle does not have an image.

21. If the vanishing line of a plane perspective is the $x$ axis, if the center of the perspective is the point $(0,-1)$, and if the image of the point $(0,\frac{1}{2})$ is the point $(0,2)$, find the equations of the transformation. What is the axis of the transformation?

We’ll follow the same procedure as outlined in #19 to find the image of a general point $P(a,b)$.

1. Find the equation of the line $PG$ $$\frac{x}{a}=\frac{y-\frac{1}{2}}{b-\frac{1}{2}}$$
2. Find the intersection of $PG$ with the vanishing line $v$. Let’s call this point $V$.
   Setting $y=0$ in the previous equation we get. $$\frac{x}{a}=\frac{-\frac{1}{2}}{b-\frac{1}{2}}$$ $$x=\frac{a}{1-2b}$$ $$⟹V=(\frac{a}{1-2b},0)$$
3. Find the slope of the line $OV$. $$slope=\frac{-1-0}{0-\frac{a}{1-2b}}$$ $$⟹slope=\frac{1-2b}{a}$$
4. Find the equation of the line through G' parallel to $OV$. By Theorem 1, $$\frac{y-2}{x}=\frac{1-2b}{a}$$ $$⟹x=\frac{a(y-2)}{1-2b}$$
5. Find the equation of the line $OP$. $$\frac{x}{a}=\frac{y+1}{b+1}$$ $$⟹x=\frac{a(y+1)}{b+1}$$
6. Find the intersection of the line from step 4 with $OP$. This will be $P^{\prime }$, the image of $P$. $$\frac{a(y-2)}{1-2b}=\frac{a(y+1)}{b+1}$$ $$⟹aby+ay-2ab-2a=ay-2aby+a-2ab$$ $$⟹3aby-3a=0$$ $$⟹3a(by-1)=0$$ $a\ne 0$ as $P$ is not on $G{G}^{\prime }$; hence $$y=\frac{1}{b}$$ To solve for x, we have two equations. $$x=\frac{a(\frac{1}{b}+1)}{b+1}$$ $$⟹(bx-a)(1+b)=0$$ and, $$x=\frac{a(\frac{1}{b}-2)}{1-2b}$$ $$⟹(bx-a)(1-2b)=0$$ For both of these to hold true simultaneously, the common term in both the equations must be zero. Hence $$x=\frac{a}{b}$$ and, $$P^{\prime }=(\frac{a}{b},\frac{1}{b}),b\ne 0$$

The axis will be the locus of points where $$a=\frac{a}{b}$$ $$⟹a(b-1)=0$$ and, $$b=\frac{1}{b}$$ $$⟹(b-1)(b+1)=0$$

For both these to be simultaneously true, the common term must be zero and hence the locus of points where $b=1$ is the axis of the given plane perspective. This is the line $y=1$.

22. Work Exercise 21, given that the image of the point $(0,2)$ is the point $(0,\frac{1}{2})$.

Let’s follow the same procedure as in the previous exercise to find the image of general point $P$.

1. Find the equation of the line $PG$ $$\frac{x}{a}=\frac{y-2}{b-2}$$
2. Find the intersection of $PG$ with the vanishing line $v$. Let’s call this point $V$.
   Setting $y=0$ in the previous equation we get. $$\frac{x}{a}=\frac{-2}{b-2}$$ $$⟹x=\frac{2a}{2-b}$$ $$⟹V=(\frac{2a}{2-b},0)$$
3. Find the slope of the line $OV$. $$slope=\frac{-1-0}{0-\frac{2a}{2-b}}$$ $$⟹slope=\frac{2-b}{2a}$$
4. Find the equation of the line through G' parallel to $OV$. By Theorem 1, $$\frac{y-\frac{1}{2}}{x}=\frac{2-b}{2a}$$ $$⟹x=\frac{a(2y-1)}{2-b}$$
5. Find the equation of the line $OP$. $$\frac{x}{a}=\frac{y+1}{b+1}$$ $$⟹x=\frac{a(y+1)}{b+1}$$
6. Find the intersection of the line from step 4 with $OP$. This will be $P^{\prime }$, $$\frac{a(2y-1)}{2-b}=\frac{a(y+1)}{b+1}$$ $a\ne 0$ as $P$ is not on $G{G}^{\prime }$; hence $$\frac{2y-1}{2-b}=\frac{y+1}{b+1}$$ $$⟹2by+2y-b-1=-by+2y-b+2$$ $$⟹3by-3=0$$ $$⟹y=\frac{1}{b}$$ To solve for x, we have two equations. $$x=\frac{a(\frac{1}{b}+1)}{b+1}$$ $$⟹(bx-a)(1+b)=0$$ and, $$⟹x=\frac{a\left(2\right(\frac{1}{b})-1)}{2-b}$$ $$⟹(bx-a)(2-b)=0$$ For both of these to hold true simultaneously, the common term in both the equations must be zero. Hence $$x=\frac{a}{b}$$ and, $$P^{\prime }=(\frac{a}{b},\frac{1}{b}),b\ne 0$$

Hmm, that’s interesting. We got the same result for $P^{\prime }$ as in #21! So this transformation is an involution where if $P^{\prime }$ is the image of $P$ then $P$ is the image of $P^{\prime }$.

23. Work Exercise 21, if the image of the point $(0,a)$ is the point $(0,b)$, determine the relation between $a$ and $b$ which will ensure that $(0,a)$ is also the image of $(0,b)$.

The image of the point $(0,a)$ according to the equations of transformation derived in #21 is $(0,\frac{1}{a})$. If the image of $(0,a)$ is $(0,b)$ then

$$b=\frac{1}{a}$$

This means if $ab=1$ then the image of $(0,a)$ is $(0,b)$.

We’ve already determined in the previous exercise that the transformation of exercise #21 is an involution and so we’re guaranteed that if $(0,b)$ is the image of $(0,a)$ then $(0,a)$ will be the image of $(0,b)$.

24. In Exercise 9, let $L$ be the point in which the line through $O$ containing a general point $P$ and its image $P^{\prime }$ intersects $l$. Prove that $\frac{\left(OL\right)\left(P{P}^{\prime }\right)}{\left(O{P}^{\prime }\right)\left(PL\right)}$ is a constant independent of $P$. Is this true if $L$ is the point in which the line $OP$ meets the vanishing line?

Errata: It should be $O{P}^{\prime }$ in the denominator instead of $OP$.

Let’s list out the coordinates of the given points $$O:(0,2)$$ $$P:(a,b)$$ $$P^{\prime }:(\frac{-3a}{2b-3},\frac{b}{2b-3})$$

The line $OP$ is

$$\frac{x}{a}=\frac{y-2}{b-2}$$

Setting $y=0$, we get $L$ as

$$L=(\frac{2a}{2-b},0)$$

Now, we can calculate the distances $OL$, $P{P}^{\prime }$, $O{P}^{\prime }$ and $PL$.

$$O{L}^2:(\frac{2a}{2-b}{)}^2+(-2{)}^2=\frac{-4b^2+16b+4a^2-16}{b^2-4b+4}$$ $$P{P}^{\prime 2}:(a-\frac{-3a}{2b-3}{)}^2+(b-\frac{b}{2b-3}{)}^2=\frac{-4b^4+16b^3-(16-4a^2)b^2}{4b^2-12b+9}$$ $$O{P}^{\prime 2}:(\frac{-3a}{2b-3}{)}^2+(\frac{b}{2b-3}-2{)}^2=\frac{-9b^2+36b+9a^2-36}{4b^2-12b+9}$$ $$P{L}^2:(\frac{2a}{2-b}-a{)}^2+(-b{)}^2=\frac{-b^4+4b^3-(4-a^2)b^2}{b^2-4b+4}$$

So the required ratio will be

$$\sqrt{\frac{\left(\frac{-4(b^2-4b-a^2+4)}{b^2-4b+4}\right)\left(\frac{-4(b^4-4b^3+(4-a^2\left)b^2\right)}{4b^2-12b+9}\right)}{\left(\frac{-9(b^2-4b-a^2+4)}{4b^2-12b+9}\right)\left(\frac{-1(b^4-4b^3+(4-a^2\left)b^2\right)}{b^2-4b+4}\right)}}$$

As all distances are finite real numbers, we can cancel out the terms to get the ratio as

$$\sqrt{\frac{16}{9}}=\frac{4}{3}$$

which is a constant independent of $P$.

If $L$ was the intersection of $OP$ and the vanishing line $y=\frac{3}{2}$, then its coordinates would be

$$L=(\frac{a}{2(2-b)},\frac{3}{2}).$$

And the distances would be $$O{L}^2:(-\frac{a}{2(2-b)}{)}^2+(2-\frac{3}{2}{)}^2=\frac{b^2-4b+a^2+4}{4b^2-16b+16}$$ $$P{L}^2:(a-\frac{a}{2(2-b)}{)}^2+(b-\frac{3}{2}{)}^2=\frac{4b^4-28b^3+4a^2{b}^2+73b^2-12a^{2}b-84b+9a^2+36}{4b^2-16b+16}$$

with $P{P}^{\prime 2}$ and $O{P}^{\prime 2}$ being the same as before.

So the ratio in this case will be $$\sqrt{\frac{\left(\frac{b^2-4b+a^2+4}{4b^2-16b+16}\right)\left(\frac{-4(b^4-4b^3+(4-a^2\left)b^2\right)}{4b^2-12b+9}\right)}{\left(\frac{-9(b^2-4b-a^2+4)}{4b^2-12b+9}\right)\left(\frac{4b^4-28b^3+4a^2{b}^2+73b^2-12a^{2}b-84b+9a^2+36}{4b^2-16b+16}\right)}}$$ $$=\frac{2}{3}\sqrt{\frac{(b^4-4b^3+(4-a^2\left)b^2\right)}{4b^4-28b^3+4a^2{b}^2+73b^2-12a^{2}b-84b+9a^2+36}}$$

which is not a constant.

25. Discuss the plane perspective transformation when the center, $O$, lies on the axis, $l$, and show, in particular, that any point and its image are still collinear with $O$.

This proof is a bit similar to the proof of Desargues' theorem where we use the line on a plane-plane intersection to prove the collinearity of points.

Let’s consider a point $A$ whose image on the picture plane is $A^{\prime \prime }$ and whose image after rabattement is $A^{\prime }$.

By the definition of a plane perspective, the points $A$, $A^{\prime }$ and $O$ all lie on the $xy$ plane ($z=0$).

As the two lines $AC$ and $OA$ intersect, they are coplanar in the plane defined by the line $AC$ and the point $O$. Let’s call this plane $\pi$. Now as $A^{\prime }{A}^{\prime \prime }$ is parallel to $OC$, with both making a ${45}^{\circ }$ angle with the $xy$ plane, they are also coplanar in the plane $\pi$.

Hence the points $A$, $A^{\prime }$ and $O$ lie on both the $xy$ plane and the plane $\pi$. So, they must line on the line of intersection of these planes. Thus they are collinear points.

This type of transformation, as we will learn later (Section 5.7), is a collineation of type V (Fig 5.3, Page 213). It has all the same characteristics as the plane perspective transformation we have discussed so far (collineations of type III) with respect to the construction of the image of a general point $P$, and the vanishing line of the plane perspective. The only difference is that these type of transformations can never be involutions (the image of a point also being its preimage), something that will be discussed in a later section.

References

---

1. MacTutor History of Mathematics archive. Girard Desargues (1591 - 1661). https://www-history.mcs.st-andrews.ac.uk/Biographies/Desargues.html ↩︎

2. Swinden, B.A. Geometry and Girard Desargues. The Mathematical Gazette. Vol. 34, No. 310 (Dec., 1950) p. 253 ↩︎

3. Wikipedia. Projective Geometry, History. https://en.wikipedia.org/wiki/Projective_geometry#History ↩︎