Please read this introduction first before looking through the solutions. Here’s a quick index to all the problems in this section.
1. Are there similarity transformations of all six types? Give an example of each possible type.
Type I
$a_{11} \ne a_{33}$
$\begin{pmatrix} a_{11} & 0 & 0 \\ 0 & -a_{11} & 0 \\ 0 & 0 & a_{33} \end{pmatrix}$
Type II
$a_{23} \ne 0$
$\begin{pmatrix} a_{11} & 0 & a_{13} \\ 0 & -a_{11} & a_{23} \\ 0 & 0 & -a_{11} \end{pmatrix}$
Type III
$a_{11} \ne a_{33}$
$\begin{pmatrix} a_{11} & 0 & 0 \\ 0 & a_{11} & 0 \\ 0 & 0 & a_{33} \end{pmatrix}$
Type IV
If we try out the possible configurations for collineations of type IV with required fixed line $x_3 = 0$ and fixed point either $(1, 0, 0)$ or $(0, 1, 0)$, we can see that neither of these can fulfill similarity constraints.
So, there are no similarities of type IV.
Type V
$a_{13} \ne 0, a_{23} \ne 0$
$\begin{pmatrix} a_{11} & 0 & a_{13} \\ 0 & a_{11} & a_{23} \\ 0 & 0 & a_{11} \end{pmatrix}$
Type VI
$\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$
2. Except in the case of triangles, equality of the measures of the corresponding angles is not a sufficient condition for the similarity of the two polygons. In view of this fact, what is the justification of calling the angle-preserving transformations of this section similarity transformations?
Two polygons are considered similar if their corresponding angles are congruent and the measures of their corresponding sides are proportional1.
We already know that similarity transformations preserve angles. Let’s find out if they preserve ratios of line segments independent of their direction.
As similarity transformations are affine, the square of the scaling factor will be $$\frac{(a_{11}^2 + a_{12}^2) + 2(a_{11}a_{12} - k^2a_{12}a_{11})m + (a_{11}^2 + a_{12}^2)m^2}{1 + m^2}$$ $$= \frac{(a_{11}^2 + a_{12}^2)(1 + m^2) + 2(a_{11}a_{12} - a_{12}a_{11})m}{1 + m^2}$$ $$= \frac{(a_{11}^2 + a_{12}^2)(1 + m^2)}{1 + m^2}$$ As $m$ is real-valued, $m^2 \ne 1$ and so the square of the scaling factor is $$a_{11}^2 + a_{12}^2$$
This quantity is independent of the direction.
Hence similarity transformations ensure that the measures of the corresponding sides of the transformed polygon are proportional to that of the original polygon. This is probably the rationale behind calling these type of transformations similarity transformations.
3. A similarity transformation of which $k=1$ is said to be direct; one for which $k=-1$ is said to be indirect. Show that the set of all direct similarity transformations is a subgroup of the group of all similarity transformations. Do the indirect similarity transformations form a group?
A direct (also called orientation preserving) similarity has the form $$\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ -a_{12} & a_{11} & a_{23} \\ 0 & 0 & a_{33} \end{pmatrix}$$
Composing two direct similarities $A$ and $B$ we get $$\begin{pmatrix} a_{11}b_{11} - a_{12}b_{12} & a_{11}b_{12} + a_{12}b_{11} & a_{13}b_{33} + a_{12}b_{23} + a_{11}b_{13} \\ -a_{11}b_{12} - a_{12}b_{11} & a_{11}b_{11} - a_{12}b_{12} & a_{23}b_{33} + a_{11}b_{23} - a_{12}b_{13} \\ 0 & 0 & a_{33}b_{33} \end{pmatrix}$$
which is clearly a direct similarity transformation.
The inverse of a direct similarity transformation $A$ is of the form $$\frac{1}{a_{12}^2a_{33} + a_{11}^2a_{33}}\begin{pmatrix} a_{11}a_{33} & -a_{12}a_{33} & a_{12}a_{23} - a_{11}a_{13} \\ a_{12}a_{33} & a_{11}a_{33} & -a_{12}a_{13} - a_{11}a_{23} \\ 0 & 0 & a_{12}^2 + a_{11}^2 \end{pmatrix}$$
which is also a direct similarity transformation.
Associativity follows from the rules of matrix multiplication and the identity transformation is the identity of the group as it is also a direct similarity transformation. Hence the set of all direct similarity transformations is a subgroup of the group of similarity transformations.
As the identity transformation is not an indirect similarity transformation, the set of indirect similarity transformations does not have an identity and hence does not form a group.
4. Show that every direct similarity transformation leaves invariant the circular points at infinity, $I:(1,i,0)$ and $J:(1,-i,0)$. Show that every indirect similarity transformation interchanges $I$ and $J$.
By solving the characteristic equation of a general direct similarity transformation, it is easy to see that the circular points at infinity are the characteristic vectors of every direct similarity transformation.
Multiplying the circular points by a general indirect transformation, we can see that it interchanges $I$ and $J$.
5. Show that the image of any circle under an arbitrary similarity transformation is a circle.
As a similarity transformation is an affine transformation, a circle can only be transformed into an ellipse. Under a similarity transformation, the scaling factor only depends on the parameters of the transformation and is independent of direction. Hence the circle will be scaled equally in all directions resulting in the image being a circle.
6. If $A$ and $A’$ are distinct points, and if $B$ and $B’$ are distinct points, show that there are exactly two similarity transformations, one direct and one indirect, which map $A$ and $A’$ and $B$ onto $B’$.
We know from #4 that the circular points at infinity are invariant under a direct similarity transformation. Hence, as we have four points and their images in total, we can uniquely determine a direct similarity transformation that maps $A$ to $A’$ and $B$ to $B’$.
We also know from #4 that the circular points at infinity are interchanged by an indirect similarity transformation. Hence, as we have four points and their images, we can uniquely determine an indirect similarity transformation that maps $A$ to $A’$ and $B$ to $B’$.
As a similarity transformation must either be direct or indirect, there can be no other similarity transformation, other than the two determined above, that achieves the given mapping.
7. (a) Find a similarity transformation which will map the triangle whose vertices are $(0,0,1)$, $(2,0,1)$, $(0,2,1)$ onto the triangle whose vertices are $(-1,0,1), (-1,1,1), (0,0,1)$.
(b) Is there a similarity transformation which will map the triangle whose vertices are $(0,0,1)$, $(2,0,1)$, $(0,1,1)$ onto the triangle whose vertices are $(-1,0,1), (-1,2,1), (-4,0,1)$?
To uniquely determine a similarity transformation, we only need to find the values of 6 parameters ($a_{11}, a_{12}, k_1a_{12}, k_1a_{11}, a_{13}, a_{23}$) for the process described in the solution to Exercise #1, Sec 5.8, and we only need 6 equations from 3 points and their images to do this.
(a) The solution to this following system of linear equations will give us the required paramaters. $$\begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 2 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 & 0 & 1 \\ 0 & 2 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 & 1 \end{pmatrix}\begin{pmatrix} a_{11} \\ a_{12} \\ a_{13} \\ -ka_{12} \\ ka_{11} \\ a_{23} \end{pmatrix} = \begin{pmatrix} -1 \\ 0 \\ -1 \\ 1 \\ 0 \\ 0 \end{pmatrix}$$
Solving this, we get the matrix of similarity to be $$\begin{pmatrix} 0 & \frac{1}{2} & -1 \\ \frac{1}{2} & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix}$$
(b) The linear system for this exercise is $$\begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 2 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \end{pmatrix}\begin{pmatrix} a_{11} \\ a_{12} \\ a_{13} \\ -ka_{12} \\ ka_{11} \\ a_{23} \end{pmatrix} = \begin{pmatrix} -1 \\ 0 \\ -1 \\ 2 \\ -4 \\ 0 \end{pmatrix}$$
Solving this we get values for $a_{12}:-3$ and $ka_{12}: -1$ that are not compatible for a similarity transformation. Hence, no similarity can achieve this mapping.
8. (a) Is there a similarity transformation which will map the square whose vertices are $(0,0,1)$, $(1,0,1)$, $(1,1,1)$, $(0,1,1)$ onto the square whose vertices are $(1,0,1)$, $(0,1,1)$, $(-1,0,1)$, $(0,-1,1)$? If so, find its equations.
(b) Is there a similarity transformation which will map the circle whose center is the origin and whose radius is $1$ onto the circle whose center is the point $(4, 3, 1)$ and whose radius is $5$? If so, find its equations.
(a) As a square is transformed into another square, the transformation is a similarity.
Taking the first three points, the linear system for this exercise is $$\begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 \end{pmatrix}\begin{pmatrix} a_{11} \\ a_{12} \\ a_{13} \\ -ka_{12} \\ ka_{11} \\ a_{23} \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1 \\ -1 \\ 0 \end{pmatrix}$$
Solving this, we get the matrix of similarity to be $$\begin{pmatrix} -1 & -1 & 1 \\ 1 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$$
Applying this similarity transform to the fourth point $(0, 1, 1)$, we get its image to be $(0, -1, 1)$ which is consistent with the given mapping.
(b) As a circle is transformed into another circle, the transformation is a similarity. Taking two points on the circle with the center and their respective images, the linear system for this exercise is $$\begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \\ -1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 & 1 \end{pmatrix}\begin{pmatrix} a_{11} \\ a_{12} \\ a_{13} \\ -ka_{12} \\ ka_{11} \\ a_{23} \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \\ 9 \\ 3 \\ -1 \\ 3 \end{pmatrix}$$
Solving this, we get the matrix of similarity to be $$\begin{pmatrix} 5 & 0 & 4 \\ 0 & 5 & 3 \\ 0 & 0 & 1 \end{pmatrix}$$
This can be interpreted as a scaling by a factor of 5 combined with a translation of $(4, 3)$.
9. By what factor is the length of a general segment altered by an arbitrary similarity transformation?
As we discovered in #2, the scaling factor of a segment under an arbitrary similarity transformation is $\sqrt{a_{11}^2 + a_{12}^2}$.
10. What conditions must be satisfied in order that a similarity transformation shall be of period 2? Give an example of such a transformation.
A similarity transformation can be interpreted as a composition of scaling, translation, rotation and reflection. Thus, for a similarity transformation to be an involution, it must either be a pure rotation about an arbitrary center by an angle of $n\pi$ where $n$ is an integer or a pure reflection. Let’s verify these claims.
Multiplying a general similarity matrix by itself we get $$\begin{pmatrix} a_{11}^2 - a_{12}^2k & a_{11}a_{12}(1 + k) & a_{12}a_{23} + a_{11}a_{13} + a_{13} \\ -a_{11}a_{12}(1 + k) & a_{11}^2 - a_{12}^2k & k(a_{11}a_{23} - a_{12}a_{13}) + a_{23} \\ 0 & 0 & 1 \end{pmatrix}$$
For this to be an involution, the following conditions must hold
$a_{11}^2 - a_{12}^2k = 1$
$a_{11}a_{12}(1 + k) = 0$
$a_{12}a_{23} + a_{11}a_{13} + a_{13} = 0$
$k(a_{11}a_{23} - a_{12}a_{13}) + a_{23} = 0$
From these conditions, we find that $a_{11} \ne 0$ for $a_{12}$ to be real.
If $a_{12} = 0$, then either
- both $a_{23}$ and $a_{13}$ must be zero with $a_{11} = 1$ leading to the identity transform, or
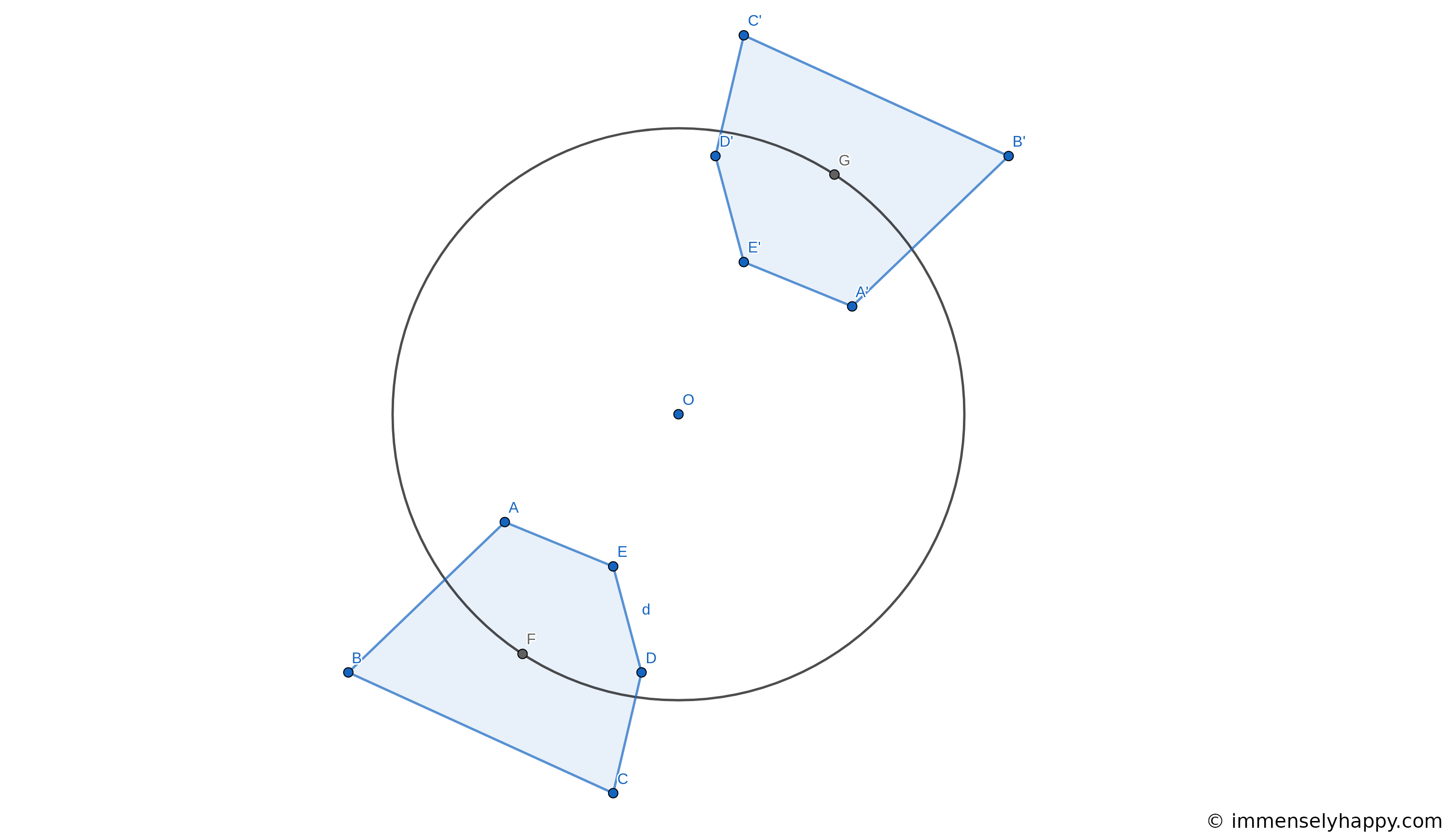
- $a_{11} = -1$ with $a_{13}$ and $a_{23}$ being allowed to take on any arbitrary value. This gives us a matrix of the form $$\begin{pmatrix} -1 & 0 & a_{13} \\ 0 & -1 & a_{23} \\ 0 & 0 & 1 \end{pmatrix}$$ which is clearly the matrix of a rotation about an arbitrary center by $n\pi$. The image below shows a polygon that has undergone this transformation.
If $k = -1$, then $a_{11}^2 + a_{12}^2 = 1$ and $a_{13} = -(a_{12}a_{23})/(1 + a_{11})$. Taking $a_{11}$ as $cos(\theta)$ and $a_{12}$ as $sin(\theta)$ we get the matrix $$\begin{pmatrix} cos(\theta) & sin(\theta) & -\frac{sin(\theta)a_{23}}{1 + cos(\theta)} \\ sin(\theta) & -cos(\theta) & a_{23} \\ 0 & 0 & 1 \end{pmatrix}$$
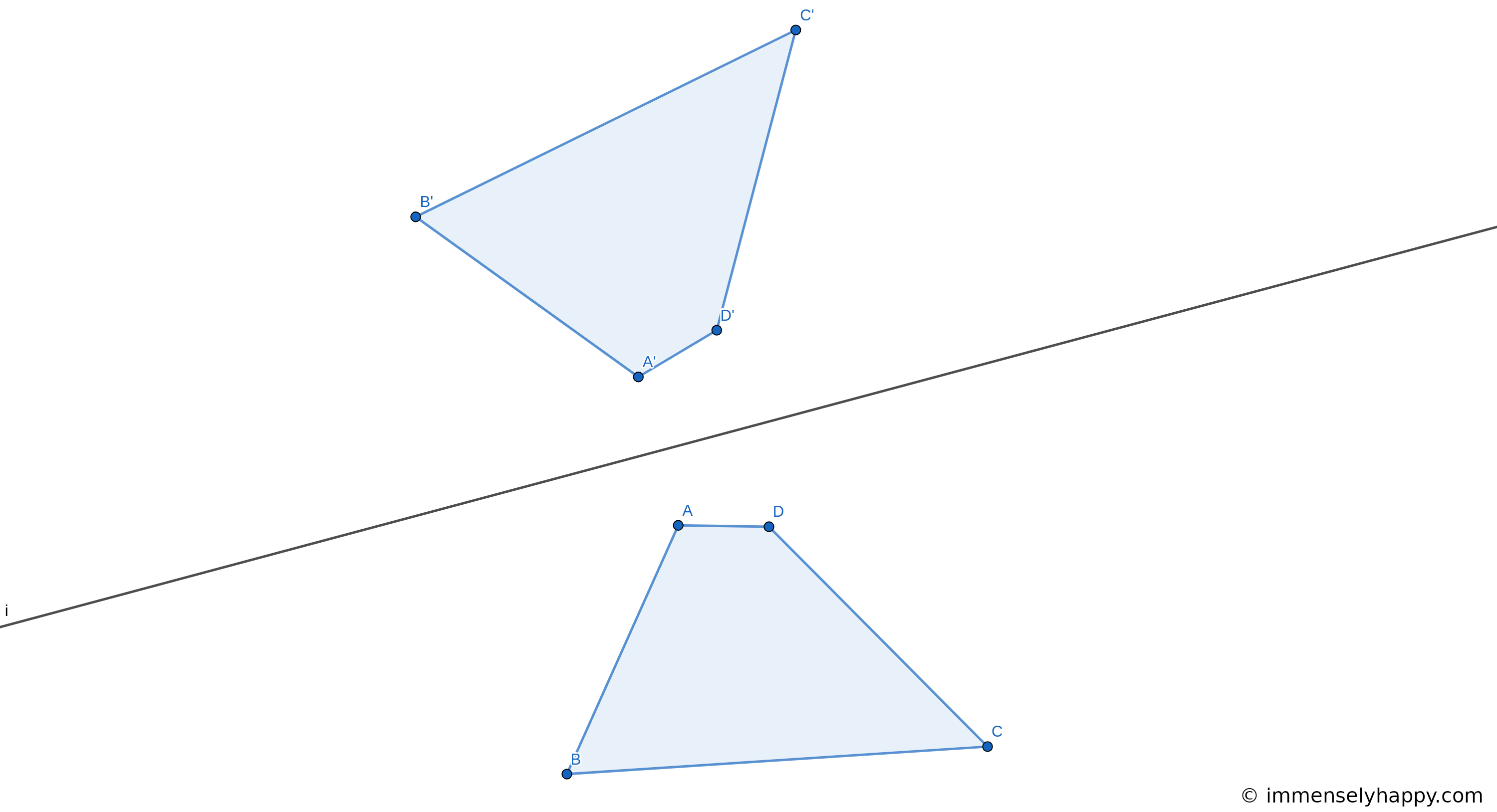
which is clearly the matrix of a reflection about an arbitrary axis. The image below shows a polygon that has undergone this transformation.
11. If $l_1 m_1 + l_2 m_2 = 0$, tan $\theta$ is undefined and the proof of Theorem 1 appears to break down. Investigate this case and show that right angles are also preserved by the general similarity transformation.
Well, he’s given us the punch line right there in the question! Two lines will be perpendicular if $l_1m_1 + l_2m_2 = 0$.
Using the equations of a general transformation and expressing this equation in terms of image coordinates we get
$$(a_{12}a_{22} + a_{11}a_{21})(l’_1m’_2 + l’_2m’_1) + \\ (a_{12}a_{32} + a_{11}a_{31})(l’_1m’_3 + l’_3m’_1) + \\ (a_{22}a_{32} + a_{21}a_{31})(l’_2m’_3 + l’_3m’_2) + \\ (a_{31}^2 + a_{32}^2)l’_3m’_3 + (a_{22}^2 + a_{21}^2)l’_2m’_2 + (a_{12}^2 + a_{11}^2)l’_1m’_1 = 0$$
If we want the transformation to preserve the $90^\circ$ angle then we expect $l’_1m’_1 + l’_2m’_2 = 0 \implies l’_1m’_1 = -l’_2m’_2$. Substituting this into the previous equation we get
$$(a_{12}a_{22} + a_{11}a_{21})(l’_1m’_2 + l’_2m’_1) + \\ (a_{12}a_{32} + a_{11}a_{31})(l’_1m’_3 + l’_3m’_1) + \\ (a_{22}a_{32} + a_{21}a_{31})(l’_2m’_3 + l’_3m’_2) + \\ (a_{31}^2 + a_{32}^2)l’_3m’_3 + (a_{22}^2 + a_{21}^2 - a_{12}^2 - a_{11}^2)l’_2m’_2 = 0$$
For this to be true for any two lines, the following must hold.
$a_{12}a_{22} + a_{11}a_{21} = 0$
$a_{12}a_{32} + a_{11}a_{31} = 0$
$a_{22}a_{32} + a_{21}a_{31} = 0$
$a_{31}^2 + a_{32}^2 = 0$
$a_{22}^2 + a_{21}^2 - a_{12}^2 - a_{11}^2 = 0$
For $a_{31}^2 + a_{32}^2 = 0$ to be true, each of $a_{31}$ and $a_{32}$ must be zero, as squares of real numbers cannot be negative.
$a_{12}a_{22} + a_{11}a_{21} = 0$, implies that $a_{12} = ka_{21}, a_{11} = ka_{22}$ for some real valued scalar $k$. Substituting this in $a_{22}^2 + a_{21}^2 - a_{12}^2 - a_{11}^2 = 0$ we get
$(1 - k^2)(a_{21}^2 + a_{22}^2) = 0$
If $a_{21}$ and $a_{22}$ were simultaneously 0 then the matrix would become singular, hence $k = \pm 1$.
These are the same constraints we obtained in the derivation of the matrix of a similarity transformation for an arbitrary angle. Hence right angles are also preserved by the general similarity transformation.
References
- Math Planet. Similarity, Polygons. https://www.mathplanet.com/education/geometry/similarity/polygons. [return]